Le circonferenze tangenti a due rette e ad una circonferenza data
Siano date due rette r ed s e un circonferenza di centro O. Vogliamo trovare le circonferenze tangenti alle rette e al cerchio dato. Proponiamo due soluzioni: la prima basata sull'uso delle omotetie, la seconda sulla cosiddetta dilatazione parallela.
Prima costruzione
Siano date due rette r ed s e un circonferenza di centro O. Consideriamo due casi, a seconda che le rette date sono tra di loro parallele (in questo caso la costruzione è molto semplice), oppure concorrenti in un punto P.
Primo caso: le rette date sono tra di loro parallele.
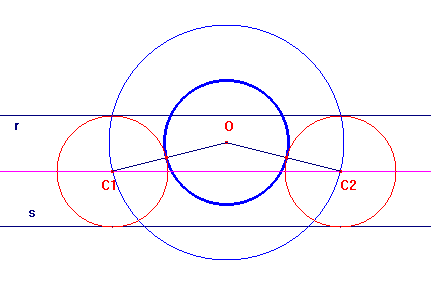
Le circonferenze cercate hanno ovviamente raggio uguale alla semidistanza tra le due rette r ed s. Basterà allora tracciare la circonferenza di centro O e raggio uguale alla somma tra il raggio della circonferenza data e questa semidistanza. Le sue intersezioni C1 e C2 con la bisettrice della striscia danno i centri delle due circonferenze che risolvono il problema. É immediato che il problema ha due soluzioni se la circonferenza data ha punti all'interno della striscia, ha una soluzione se è esternamente tangente ad una delle due rette date, non ha soluzioni se è esterna alla striscia.
Secondo caso: le due rette date sono incidenti in un punto P.
Date le rette r ed s e la circonferenza di centro O, consideriamo il rombo ABCD avente i lati tangenti al cerchio dato e paralleli alle rette date. La retta che passa per P e per uno dei quattro vertici del rombo interseca la circonferenza data in non più di due punti: nella figura qui sotto abbiamo considerato la retta PC che ha due intersezioni C' e C". L'omotetia di centro C' e rapporto uguale al rapporto delle misure con segno dei segmenti orientati C'P e C'C, muta la circonferenza data in una della circonferenze richieste, tangente in C' alla circonferenza data. L'analogo discorso con C'' produce un'altra circonferenza che risolve il problema.
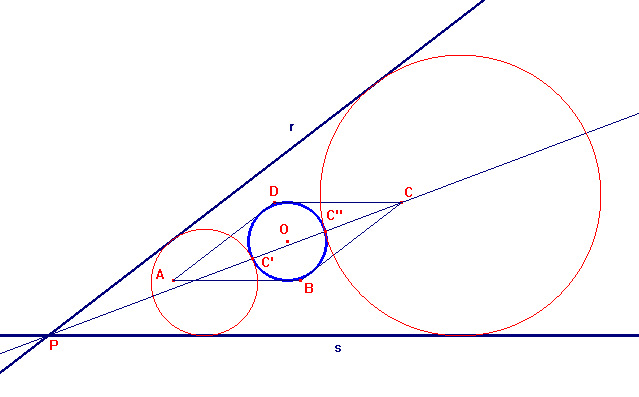
É allora facile concludere che ci saranno al massimo otto soluzioni (se la circonferenza data è secante entrambe le rette date), sei soluzioni se una è tangente e l'altra secante, quattro negli altri casi (per esempio quella nella figura qui sopra).
Puoi vedere un'animazione con CabriJava, costruita utilizzando la tecnica appena descritta.
Seconda costruzione
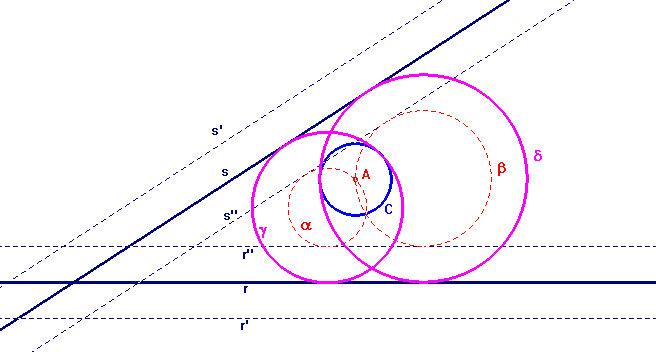
Questa seconda costruzione utilizza una particolare trasformazione geometrica, che alcuni chiamano dilatazione parallela: si immagina che il raggio r del cerchio dato si riduca a zero (il cerchio è ridotto al suo centro), mentre le rette rimangono parallele con distanze dal centro del cerchio che si è ridotto a zero aumentate o diminuite di r. Si é così ricondotti al caso di un punto e due rette e si può applicare una delle tecniche viste in quel caso. Nella figura qui sotto abbiamo costruito solo due delle possibili circonferenze, per non ingombrare troppo il disegno. C è il cerchio dato, che si riduce al suo centro A, r ed s le rette date, che traslano nelle rette tratteggiate indicate. Le circonferenze che passano per A e sono tangenti alle rette, per esempio, r" ed s", sono α e β. Due delle circonferenze finali cercate sono γ e δ.