Premessa e presentazione del problema
In questa monografia è trattato il famoso "problema di Apollonio": date tre circonferenze, eventualmente degeneri, trovare le circonferenze tangenti a tutte tre. Per circonferenze degeneri si intendono quelle aventi raggio zero (i punti) o raggio infinito (le rette).
Nel caso di tre punti o di tre rette il problema era già stato proposto, e risolto, da Euclide in connessione con i cerchi inscritti e circoscritti ad un triangolo (libro III degli Elementi). Apollonio si pone il problema generalizzato della stessa costruzione, con riga e compasso, quando i tre oggetti dati sono circonferenze, eventualmente degeneri. Un'intera opera, in due volumi, è dedicata a questo problema: si tratta delle Tangenze. L'opera è andata purtroppo interamente persa, e ne possiamo ricostruire parzialmente il contenuto solo attraverso le citazioni di Pappo. Essa era costituita da due volumi, nel primo dei quali venivano riproposti i due casi già trattati da Euclide assieme ad altri sei, mentre nel secondo venivano trattati i due casi più difficili: due rette e un cerchio, e tre cerchi.
La difficoltà del problema più generale, e il fatto che numerosi tentativi ripetuti fino al secolo XVI fossero andati a vuoto, avevano fatto ritenere ai matematici che in realtà Apollonio non avesse risolto il problema: questo problema era considerato da molti come una vera e propria sfida alla propria abilità.
I matematici arabi, soprattutto Ibrahim ibn Sinan (909-946) e Ibn al-Haytham (965-1041) avevano trovato una soluzione algebrica. Nel XVI secolo Regiomontano tentò di risolverlo utilizzando le sezioni coniche. Successivamente importanti ricerche, comprendenti anche costruzioni con riga e compasso, sono dovute, tra gli altri, a F.Viète (Apollonius Gallus, Parigi, 1600), P.Fermat (De contactibus sphaericis, Varia opera mathematica, Tolosa 1679), I. Newton (Philosophiae naturalis principia mathematica, Londra, 1687) e a molti altri matematici successivi (L.Eulero, S.D.Poisson, N.Fuss, G.Monge, J.Binet, P.Hachette, L.Gaultier, J.D.Gergonne, J.V.Poncelet, J.Steiner, J.Plücker, E.Study). Una interessante discussione e la trattazione di alcuni casi si trovano nelle lettere scritte da Cartesio nel novembre 1643 alla sua allieva favorita, la principessa Elisabetta, figlia del re Federico di Boemia. Gli studi su questo problema hanno dato impulso a molte ricerche e scoperte in geometria, sia sintetica che analitica. Sono state pubblicate più di 100 soluzioni diverse.
Il problema può essere formulato come segue: dati tre oggetti, punti rette o circonferenze, costruire, con riga e compasso, le circonferenze tangenti ai tre oggetti dati, con la convenzione che la tangenza ad un punto equivalga al passaggio per il punto.
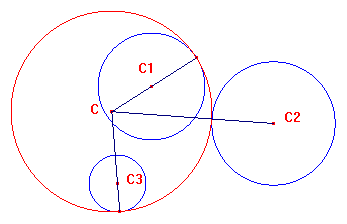
In termini di geometria analitica il problema, nel suo caso più generale, può essere posto nei seguenti termini. Date tre circonferenze di raggi r1, r2, r3 e centri C1(x1,y1), C2(x2,y2), C3(x 3,y3), le circonferenze tangenti cercate hanno un raggio r ed un centro C(x,y) tali che
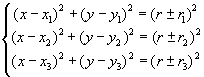 ,
,
Le alternative di segno possono essere prese, nelle tre equazioni, indipendentemente una dall'altra. Si hanno così otto possibili sistemi di equazioni nelle incognite x, y, r. Con opportune sottrazioni tra le equazioni ogni sistema può essere ricondotto ad uno di primo grado, per cui al massimo si avranno otto distinti sistemi e otto soluzioni.
Il numero massimo di soluzioni varia comunque a seconda del tipo di oggetti dati, secondo la tabella seguente:
| Tipo di oggetti | Numero massimo di soluzioni |
| Tre cerchi | Otto soluzioni |
| Due cerchi e una retta | Otto soluzioni |
| Due cerchi e un punto | Quattro soluzioni |
| Un cerchio e due rette | Otto soluzioni |
| Un cerchio, una retta e una punto | Quattro soluzioni |
| Un cerchio e due punti | Due soluzioni |
| Tre rette | Quattro soluzioni |
| Due rette e un punto | Due soluzioni |
| Una retta e due punti | Due soluzioni |
| Tre punti | Una soluzione |
Dal punto di vista della costruibilità con riga e compasso si osservi che, se in uno dei sistemi si sottrae un'equazione dalle altre due, si ottiene un'equazione di primo grado da cui si può ricavare x ed y in funzione di r; sostituendo nella equazione rimanente si ottiene un'equazione di secondo grado in r: allora le incognite possono essere espresse in termini di radicali quadratici in funzione dei centri e raggi dati. Ciò significa che la costruzione è effettuabile con riga e compasso.
Nelle pagine che seguono sono trattate con un certo dettaglio le costruzioni in tutti i dieci casi possibili. In molti casi sono proposte diverse costruzioni, anche se, come per tutti i problemi di tangenza tra rette e circoli, spesso il metodo più semplice di soluzione è l'uso dell'inversione circolare. Questo metodo è poi particolarmente elegante e immediato quando almeno uno dei tre oggetti dati è un punto.
In ogni caso in questa monografia non intendiamo fare una trattazione completa di questo problema (trattazione che richiederebbe probabilmente centinaia di pagine), ma solo proporre alcune tecniche tecniche risolutive, per lo più senza le dimostrazioni. Come preliminare al problema proponiamo anche la trattazione del caso n=2: le circonferenze tangenti a due circonferenze, eventualmente degeneri. E' chiaro che questo problema ha infinite soluzioni e le soluzioni del caso n=3 sono comprese tra queste.
Una trattazione dello stesso problema, comprensiva anche delle tecniche per costruire le figure con il pacchetto PSTricks di LaTeX si può trovare, in questo stesso sito, in una monografia dal titolo Apollonio, inversioni e PSTricks.