Le circonferenze tangenti a due circonferenze, eventualmente degeneri
Trattiamo questo caso come premessa al problema di Apollonio vero e proprio in cui gli oggetti dati sono tre circonferenze, eventualmente degeneri. E' chiaro che, nel caso gli oggetti dati siano invece solo due, le soluzioni sono di norma infinite e tra esse ci saranno quelle (al massimo otto) che soddisfano il problema di Apollonio. Considereremo le varie situazioni che si possono presentare, secondo il tipo degli oggetti dati.
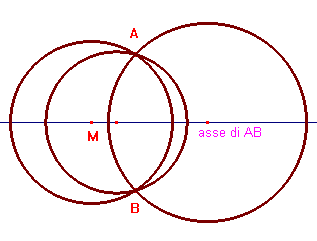
Due punti
La soluzione in questo caso è banale e basta considerare le circonferenze che hanno centro sull'asse del segmento AB che congiunge i due punti dati. L'insieme delle circonferenze è costituito dal fascio delle circonferenze passanti per A e B. Si veda un'animazione con CabriJava.
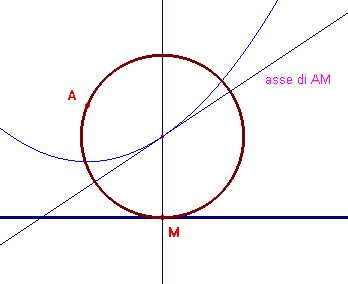
Un punto e una retta
Supponendo che il punto dato A sia fuori della retta, il centro delle circonferenze cercate sta sulla parabola di fuoco A e direttrice la retta data. Preso un punto M sulla retta data, basta tirare la perpendicolare per M alla retta e l'asse del segmento AM. Si veda un'animazione con CabriJava.
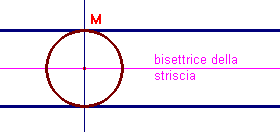
Due rette
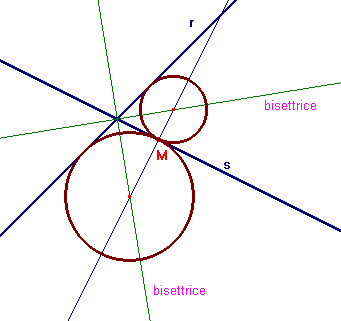
Nel caso le due rette siano parallele le circonferenze cercate hanno centro sulla bisettrice della striscia, nel caso le due rette non siano parallele hanno centro sulle bisettrici degli angoli individuati dalle due rette. Basta prendere un punto M su una delle due rette e tirare la perpendicolare alla retta scelta. Si veda un'animazione con CabriJava.
Un punto e un cerchio
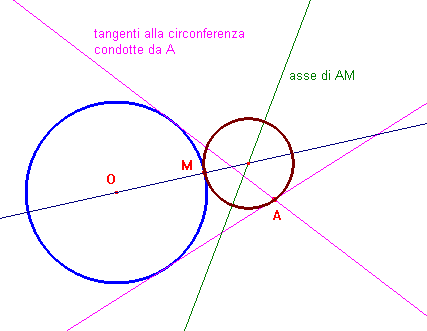
Preso un punto M sulla circonferenza di centro O data, si traccia la retta OM e l'asse del segmento AM. Il centro della circonferenza cercata sta nell'intersezione di queste due rette. Le circonferenze cercate si riducono alle tangenti condotte da A, nel caso M coincida con uno dei due punti di tangenza. La stessa costruzione funziona anche con A interno al cerchio dato. Si veda un'animazione con Cabrijava.
Una retta e un cerchio
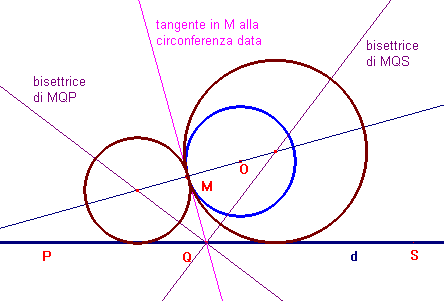
Data la circonferenza di centro O e la retta d, si prende un punto M su circonferenza O. Da M si conduce la tangente alla circonferenza data che incontra la d in Q. Le circonferenze cercate hanno il centro sull'intersezione tra la retta OM e le bisettrici degli angoli MQP, MQS. Si veda un'animazione con CabriJava.
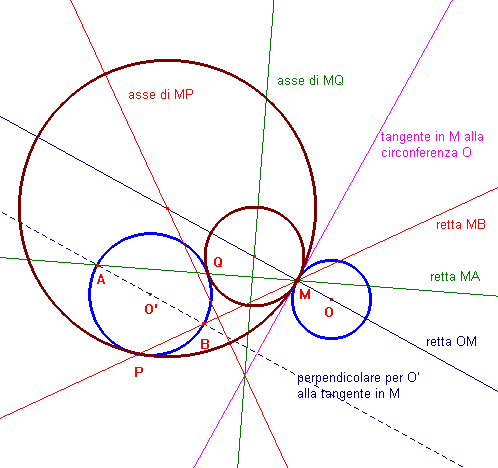
Due cerchi
Date le due circonferenze O ed O', si considera un punto M sulla circonferenza O e la tangente alla stessa, passante per M. Le circonferenze cercate saranno tangenti al cerchio O' e alla predetta tangente. Si è ricondotti al caso di una retta e un cerchio, solo che questa volta il punto di tangenza dato, M, è sulla retta anziché sul cerchio, come qui sopra. Si può usare una diversa tecnica, deducibile dalla figura successiva. Si tira la perpendicolare per O' alla retta tangente trovata prima; essa interseca la circonferenza O' in A e B. Le rette MA e MB incontrano la circonferenza O' ulteriormente in Q e P. I centri delle circonferenze cercate stanno sull'intersezione degli assi di MP ed MQ con la retta OM. Si veda un'animazione con CabriJava.