Osservazioni sui modelli di Klein e Poincaré
I due modelli proposti per la geometria iperbolica (Klein e Poincaré) sono equivalenti, nel senso che possono essere trasformati uno nell'altro. Esistono anche altri modelli della stessa geometria (sempre a Poincaré è legato un modello in cui gli enti sono rappresentati in un semipiano, anziché in un cerchio).
Quello che qui comunque ci interessa segnalare è che ci possono essere diversi modelli che rappresentano "visivamente" gli stessi oggetti. Questo fatto è particolarmente importante per capire il significato di enti primitivi e di assiomi: quello che conta non è l'idea intuitiva che noi ci possiamo fare degli oggetti di cui parliamo, ma solo i rapporti che tra essi intercorrono, e che sono precisati dagli assiomi.
Nei due modelli le figure geometriche appaiono completamente diverse (segmenti ↔ archi di cerchio, cerchi ↔ ovali, ecc.), ma le proprietà che le caratterizzano sono le stesse: per due punti passa una sola retta, per un punto fuori da una retta si possono condurre due parallele ad una retta data, la somma degli angoli interni di un triangolo è sempre minore di 180°, ecc.
C'è anche un'altra osservazione interessante che si può fare su questi modelli, anche se è più semplice da capire sul modello di Klein. In questo modello ciò che rende possibile condurre per un punto fuori da una retta infinite rette non secanti la retta data è legato alla limitatezza del disco su cui si rappresentano gli oggetti. E' chiaro che se costruiamo in un modello con un dato disco due rette non secanti e poi immaginiamo di ingrandire opportunamente il disco lasciando ferme le rappresentazioni delle due rette, esse potranno incontrarsi.
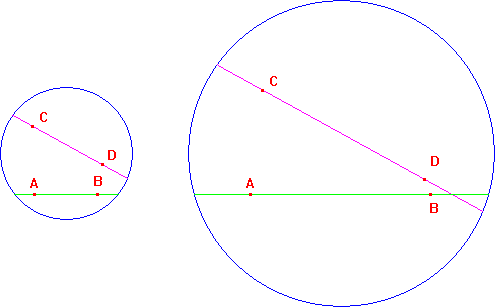
Possiamo chiamare orizzonte, come si fa usualmente, la circonferenza che delimita il disco. In sostanza il piano di Euclide può essere pensato come il disco di Klein in cui l'orizzonte si è allontanato indefinitamente. E' chiaro che aumentando le dimensioni del disco il numero di rette non secanti una data retta diminuisce, ma resta pur sempre infinito, qualunque sia la distanza dell'orizzonte. E' solo nel preciso "istante" in cui la distanza dell'orizzonte diventa infinita che, almeno così sembra, di tali rette ne dovrebbe rimanere una sola. Il problema è che una tale situazione non è fisicamente sperimentabile (non esiste un "preciso istante" in cui la distanza diventa infinita, cioè in cui si passa da infinite rette non secanti ad una sola) e quindi è ben lungi dal poter essere considerata intuitiva!