David Hilbert e gli Assiomi della Geometria

David Hilbert nasce a Koenigsberg, Prussia (ora Kaliningrad, Russia) nel 1862 e muore a Goettingen, Germania, nel 1943. Uno dei più eminenti matematici a cavallo tra l'800 e il 900, pubblicò, nel 1899, il Grundlagen der Geometrie (Fondamenti della geometria), sicuramente il libro che ebbe la più grande influenza in questo campo, dopo Euclide. Tra gli innumerevoli suoi contributi fondamentali ai vari campi della matematica ricordiamo solo i 23 Problemi, proposti nel Secondo Congresso Internazionale di Matematici, a Parigi nel 1900, alcuni dei quali sono ancora insoluti.

Hilbert propone una assiomatizzazione della geometria, che tiene conto delle scoperte delle nuove geometrie non euclidee e del dibattito sugli Elementi nato quasi subito dopo la loro pubblicazione. L'idea è quella di stabilire per la geometria un sistema di assiomi completo e semplice quanto più possibile e di dedurre, dai medesimi, le proposizioni geometriche più importanti, in modo da mettere in luce il significato dei diversi assiomi e la portata delle conseguenze da trarre da essi. Questo è quanto lo stesso Hilbert afferma nella presentazione della sua opera:

La differenza sostanziale tra gli assiomi di Hilbert e quelli di Euclide è che essi non esprimono nessun contenuto che non sia quello delle loro mutue relazioni di tipo puramente logico. Cioè gli assiomi non sono verità evidenti, ma definizioni implicite dei termini primitivi che essi contengono.

Riportiamo, per un utile confronto con il sistema di Euclide, gli Assiomi di Hilbert, segnalando che sono qui raggruppati in successione, mentre nel testo dei Grundlagen dopo ogni gruppo di assiomi Hilbert dà una serie di teoremi che dipendono da quegli assiomi. Anche noi seguiremo, seppure molto sommariamente, questa strada nella presentazione dettagliata dei fondamenti della geometria.

Termini non definiti

• Punti
• Rette
• Piani
• Giace su, contiene
• Tra
• Congruente

Assiomi di incidenza

• Dati due punti qualsiasi A, B esiste una retta a che contiene entrambi i punti A, B.
• Dati due punti qualsiasi A, B non esiste più una retta che contiene entrambi i punti A, B.
• Esistono almeno due punti su una retta. Esistono almeno tre punti che non giacciono su una retta.
• Dati tre punti qualsiasi  A, B, C che non giacciono sulla stessa retta esiste un piano α che contiene ciascuno dei tre punti A, B, C. Per ogni piano esiste un punto che gli appartiene.
• Dati tre punti qualsiasi A, B, C che non giacciono sulla stessa retta esiste non più di un piano che contiene ciascuno dei tre punti A, B, C.
• Se due punti A, B di una retta a giacciono su un piano α allora ogni punto di a giace sul piano α.
• Se due piani α, β hanno un punto A in comune, allora essi hanno almeno un altro punto B in comune.
• Esistono almeno 4 punti che non giacciono su un piano.

Assiomi di ordine

• Se un punto B giace tra un punto A e un punto C allora i punti A, B, C sono tre distinti punti di una retta e B giace anche tra C ed A.
• Dati due punti A e C, esiste sempre almeno un punto B sulla retta AC tale che C giace tra A e B.
• Dati tre punti su una retta esiste non più di un punto che giace tra gli altri due.
• Siano A, B, C tre punti che non giacciono su una retta e sia a una retta nel piano ABC che non incontra nessuno dei tre punti A, B, C. Se la retta a passa per un punto del segmento AB, passa anche per un punto del segmento AC, o per un punto del segmento BC.

Assiomi di congruenza

• Se A, B sono due punti su una retta a, e A' è un punto sulla stessa o un'altra retta a' allora è sempre possibile trovare un punto B' su un dato lato della linea a' tale che AB e A'B'  siano congruenti.
• Se un segmento A'B' e un segmento A"B" sono congruenti allo stesso segmento AB, allora i segmenti A'B' e A"B" sono congruenti tra di loro.
• Su una retta a siano AB e BC due segmenti che, eccettuato B, non hanno punti in comune. Inoltre, sulla stessa o un'altra retta a', siano A'B' e B'C' due segmenti che, eccettuato B', non hanno punti in comune. In questo caso, se AB è congruente ad A'B' e BC è congruente a B'C', allora AC è congruente ad A'C'.
• Se 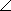ABC è un angolo e B'C' è un raggio, allora esiste esattamente un raggio B'A' su ogni lato della retta B'C' tale che 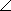A'B'C' e 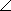ABC siano congruenti. Inoltre ogni angolo è congruente a se stesso.
• Se per due triangoli ABC e A'B'C' vale che AB è congruente ad A'B', AC è congruente ad A'C' e 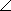BAC è congruente a 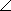B'A'C', allora anche gli angoli 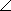ABC e 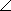A'B'C' sono congruenti.

Assioma di parallelismo

• Sia a una retta ed A un punto fuori di essa. Allora esiste al più una retta nel piano che contiene a ed A, che passa per A e non interseca a.

Assiomi di continuità

• Se AB e CD sono due segmenti, esiste un numero n tale che n copie di CD costruite consecutivamente da A lungo il raggio AB andranno oltre il punto B (Assioma di Archimede).
• E' impossibile ampliare un insieme di punti su una retta con il suo ordine e con relazioni di congruenza che conservino le relazioni esistenti tra gli elementi originali e gli assiomi di ordine e congruenza sulla retta (Assioma di continuità ).

Scopo di questa introduzione ai fondamenti della geometria è proprio quello di presentare con un certo dettaglio (ma senza alcuna pretesa di completezza e sistematicità) gli assiomi di Hilbert della geometria e le loro più immediate conseguenze.