Giochiamo con Gauss - Help
Questo programma risolve un sistema lineare di m equazioni in n incognite, con il metodo della riduzione a scala di Gauss Jordan. Consente di risolvere un sistema costituito da un massimo di 10 equazioni in 10 incognite, anche se questa limitazione è fatta solo per motivi di semplicità: il codice potrebbe essere applicato ad un numero qualunque di equazioni e di incognite, ma si rischia di superare facilmente i limiti di calcolo tipici di Javascript. In ogni caso chi ha voglia di provare può modificare i valori massimi di m ed n contenuti nelle righe opportune del codice html della pagina.
Si richiede preventivamente l'indicazione del numero di equazioni e di incognite di cui sarà costituito il sistema.
Successivamente occorre introdurre i coefficienti. Sono consentiti solo coefficienti razionali, introdotti nella forma: (-)numeratore(/denominatore), dove le parentesi indicano oggetti opzionali e dove numeratore e denominatore devono essere numeri naturali. Per passare da una casella all'altra si può usare il mouse o il tasto di tabulazione.
Introdotti i coefficienti il codice esegue, alla pressione del tasto apposito, un controllo dell'accettabilità dei valori introdotti. Se necessario viene sempre eseguita anche una riduzione delle frazioni ai minimi termini.
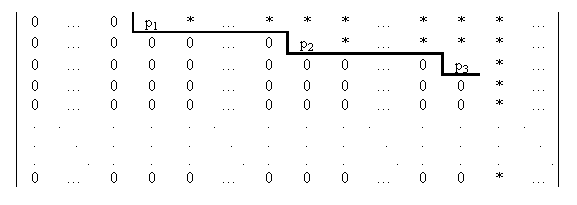
Si può a questo punto iniziare la risoluzione, tenendo conto che l'obiettivo finale è quello di ottenere un sistema nella forma cosiddetta a scala, che, nella sua forma più generale, ha una matrice dei coefficienti (matrice incompleta) con il seguente aspetto:
,
dove i numeri p1, p2, ecc. si chiamano pivot, e dove le ultime righe possono essere eventualmente tutte nulle.
Il numero dei pivot si chiama rango del sistema e lo si indica con r. E' chiaro che il sistema ha soluzioni se e solo se, in corrispondenza alle eventuali ultime m-r righe tutte nulle, anche i termini noti (che non compaiono nella matrice sopra riportata) sono tutti nulli. Se il sistema ha soluzioni, le incognite che non corrispondono a colonne in cui si trovano i pivot sono completamente arbitrarie e si dice che il sistema ha ∞ n-r soluzioni, con la convenzione che ∞ 0 significhi 1. Quando il sistema è ridotto a scala la sua soluzione è immediata: si procede all'indietro, determinando le incognite che compaiono nell'ultima equazione utile e si risale via via fino a trovare tutte le incognite.
Per ottenere la riduzione a scala si procede con le seguenti operazioni:
-
Si ricerca qual è la prima colonna non tutta nulla (abitualmente nessuna colonna è tutta nulla, altrimenti l'incognita corrispondente è "inutile", ma abbiamo preferito metterci nella situazione più generale possibile).
-
Si opera, eventualmente con uno scambio di righe, in modo che sulla prima riga, in corrispondenza alla prima colonna non nulla, ci sia un numero diverso da zero: questo numero prende il nome di pivot numero 1 o p1.
-
Con una opportuna combinazione lineare tra righe si fa in modo che dalla seconda riga in poi, sotto al pivot, compaiano solo zeri. Per fare questo si usa fare la seguente combinazione lineare: se la riga i ha, sotto al pivot p1, l'elemento a non nullo, si sostituisce la riga i con la combinazione seguente ottenuta sommando la riga i con la riga 1 moltiplicata per
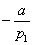. E' chiaro che non è l'unica
scelta possibile, ma questa ha il vantaggio, se la matrice
è quadrata, di non modificare il determinante della
matrice. Se si tiene conto che l'operazione precedente
può al più, sempre per le matrici quadrate,
cambiare di segno il determinante, si capisce come questa
tecnica possa essere vantaggiosamente applicata anche al
calcolo dei determinanti.
-
Si ripetono le operazioni indicate, considerando la matrice che si ottiene da quella così trasformata sopprimendo la prima riga.
Il programma qui proposto funziona proprio su questo principio, chiedendo l'intervento diretto dell'utente ad ogni passo e fornendo, in automatico, solo l'eventuale moltiplicatore necessario per eseguire la terza operazione richiesta. Il programma può anche fornire la soluzione del sistema, ma solo dopo che esso è stato ridotto a scala.
E' facile che, per sistemi con elevato numero di equazioni o di incognite, il metodo di Gauss Jordan provochi errori di overflow, in quanto i numeri interi coinvolti possono rapidamente superare le 15 cifre massime previste. Purtroppo questi errori non sono segnalati dall'interprete. Evitate quindi di introdurre coefficienti grandi e, in ogni caso, controllate l'attendibilità di soluzioni quando i valori coinvolti sono alti (non solo a livello delle soluzioni presentate, ma anche a livello dei numeri che compaiono nel sistema ridotto a scala).
Solo per i più pigri abbiamo implementato anche una versione completamente automatica di questo codice.
Buon lavoro con i sistemi lineari, la bestia nera di molti studenti di algebra lineare (e se si prova a risolvere un sistema di sole dieci equazioni in dieci incognite, con inserimento casuale dei coefficienti, e si esaminano le soluzioni, si capisce perché...)!