Il teorema di Pascal e le coniche per 5 punti
In questa pagina vogliamo esaminare come si possa utilizzare il teorema di Pascal sulle coniche per costruire una conica passante per 5 punti, come luogo geometrico.
Questo famoso teorema fu scoperto da Blaise Pascal (1623-1662) all'età di 16 anni e pubblicato nell'opera Essay pour le coniques, a Parigi, nel 1640. Ben presto dimenticato, fu riscoperto da Ch. Bossut, che pubblicò nel 1779 un'edizione delle opere di Pascal. Il teorema è noto come Hexagrammum Mysticum e la cosa non deve affatto stupire se si pensa che da questo teorema Pascal derivò tutte le proprietà dimostrate da Apollonio sulle coniche, oltre a molti altri risultati, in totale almeno 400 proposizioni!
L'enunciato del teorema è il seguente:
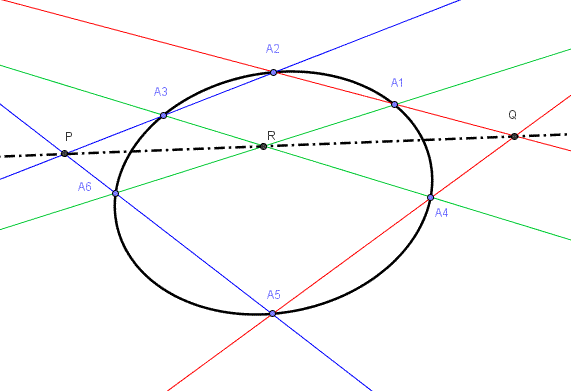
Considerati sei punti qualunque su una conica, \(A_1,A_2,A_3,A_4,A_5,A_6\), i punti di intersezione delle coppie di lati "opposti" \(A_1A_2\) e \(A_4A_5\), \(A_2A_3\) e \(A_5A_6\), \(A_3A_4\) e \(A_6A_1\), sono allineati.
La retta che contiene questi punti di intersezione si chiama anche retta di Pascal. È opportuno ricordare che la verifica dell'allineamento di tre o più punti ottenuti con diverse costruzioni è molto spesso una cosa di grande importanza in matematica. Un altro esempio di questo si ha nella retta di Eulero per un triangolo, che è la retta che contiene il baricentro, l'ortocentro e il circocentro di un qualunque triangolo.
L'immagine che segue mostra la situazione nel caso di un'ellisse: la retta di Pascal è la retta per \(P,Q,R\).
Puoi anche controllare che l'ordine in cui sono presi i punti è assolutamente ininfluente nell'animazione sul Teorema di Pascal.
Qui vogliamo mostrare come si possa usare il teorema di Pascal per costruire per punti (e quindi come luogo geometrico) l'unica conica passante per cinque punti dati. Che per cinque punti passi una ed una sola conica è una proprietà che pare fosse già nota ad Apollonio. In ogni caso la cosa è, con la geometria analitica, di immediata dimostrazione se si tiene conto che l'equazione cartesiana di una conica è un'equazione di secondo grado in due incognite, cioè un'equazione del tipo \[Ax^2+Bxy+Cy^2+Dx+Ey+F=0\,:\] si tratta dunque di un'equazione in cui compaiono sei parametri, cinque soli dei quali sono indipendenti (in quanto almeno uno dei primi tre deve essere diverso da zero).
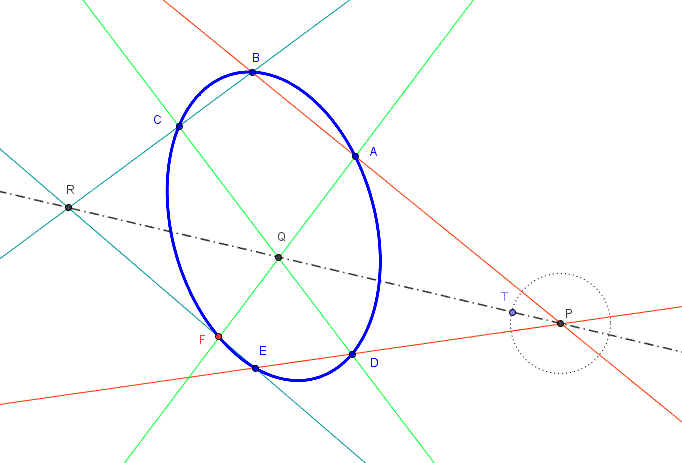
La costruzione si basa sulla seguente idea: dati cinque punti \(A,B,C,D,E\), determiniamo un sesto punto, \(F\), della conica passante per i cinque punti dati, e costruiamo la conica facendo variare \(F\).
Lo schema dei passaggi da eseguire è il seguente.
- Consideriamo cinque punti \(A,B,C,D,E\).
- Determiniamo, se esiste, il punto \(P\) di intersezione delle rette \(AB\) e \(DE\): la retta di Pascal dovrà passare per \(P\).
- Poiché siamo interessati alla costruzione della conica come luogo geometrico, e il luogo sarà ottenuto facendo variare la retta di Pascal, prendiamo una circonferenza di centro \(P\) e raggio qualunque, per esempio 1, e su di essa un punto \(T\), che sarà il punto base per la generazione del luogo.
- Costruiamo la retta \(PT\).
- Indichiamo con \(Q\) il punto di intersezione di \(PT\) con \(CD\): per il teorema di Pascal anche la retta \(AF\) (\(F\) è il punto da determinare) dovrà passare per \(Q\). Costruiamo allora questa retta \(AQ\) che conterrà il punto \(F\).
- Indichiamo con \(R\) il punto di intersezione di \(PT\) con \(BC\): sempre per il teorema di Pascal anche la retta \(EF\) dovrà passare per \(R\). Costruiamo allora questa retta \(ER\) che conterrà il punto \(F\).
- A questo punto \(F\) è semplicemente l'intersezione tra \(AQ\) ed \(ER\).
- Il luogo descritto da \(F\) al variare di \(T\) è la conica cercata.
La figura qui di seguito mostra la costruzione. Puoi anche vedere un'animazione della stessa costruzione.