Un problema di cinematica a prima vista banale
Consideriamo il seguente problema:
Due treni partono da due città
distanti tra loro 6 km e si muovono, uno verso l'altro, alla
velocità di 3 km/h. Un uccellino parte dal primo treno e
vola, alla velocità costante di 6 km/h, da un treno
all'altro e viceversa, fino all'incontro tra i treni. Si
chiede lo spazio percorso dall'uccellino e il diagramma
orario dei tre moti.
É ovvio che la risposta alla prima domanda è banale: poiché i treni impiegano un'ora per incontrarsi, l'uccellino avrà percorso esattamente 6 km.
Altrettanto semplice può dirsi la determinazione del diagramma orario del moto dei due treni. Indichiamo con A il primo treno, con B il secondo, e introduciamo un sistema di ascisse con l'origine in A e orientato verso B. Utilizziamo le ore come unità di misura dei tempi e i km come unità di misura degli spazi.
In questo sistema il diagramma orario del moto dei due treni è, rispettivamente, xA=3t e xB=-3t+6. La loro rappresentazione grafica, che mette in evidenza anche il momento dell'incontro, è rappresentata qui sotto.
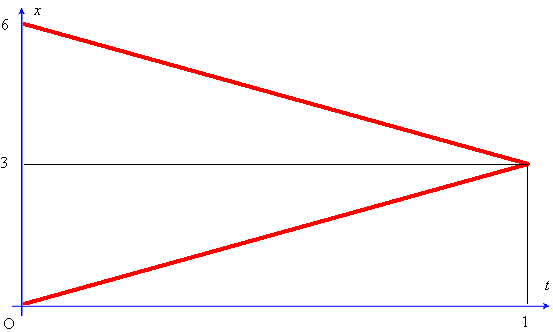
Esaminiamo ora il moto dell'uccellino. Il diagramma orario,
prima dell'incontro con il treno B, è chiaramente
xU=6t. Per trovare il momento d'incontro
con il treno B basterà risolvere il sistema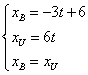 
, e si trova subito 
. Il diagramma
orario da questo istante fino al nuovo incontro con il treno A
sarà del tipo 
, e q andrà
determinato con la condizione che. per 
, si
abbia x=4. Si trova facilmente q=8, da
cui 
. Procedendo come prima si trova
che l'incontro con il treno A avviene a 
e 
. Il diagramma orario del moto dell'uccellino
sarà, da questo momento e fino all'incontro con il
treno B, 
. Si possono così trovare
l'istante ed il posto del nuovo incontro con il treno B:
. Iterando il procedimento si trovano, di seguito,
i seguenti diagrammi orari: 
, 
, 
, ecc. I coefficienti angolari di questi diagrammi
sono, alternativamente, 6 e -6, a seconda che l'uccellino
voli verso B o verso A. Tenendo conto di queste equazioni si
trovano facilmente gli istanti e le ascisse successive di
incontro. Se riportiamo anche quelli già trovati,
abbiamo:
tempi: 
..., ascisse: 
... .
I tempi sono tutti del tipo 
, le ascisse del tipo
(con il +1 per gli incontri con il treno B, il -1
per quelli con il treno A), avendo indicato con n il
numero progressivo dell'incontro. Si vede subito come, dal
punto di vista teorico, il numero di incontri dell'uccellino
con i treni, prima dello scontro, è infinito, e come il
tempo finale tende ad 1, mentre la ascissa tende a 3. É
altresì evidente che i "voli" diventano sempre
più brevi.
Gli spazi percorsi dall'uccellino sono, infatti,
nell'ordine, 
..., e la somma di questi
termini dà proprio 6. (Si tratta di una serie geometrica,
di ragione 
, in cui ciascun termine è
moltiplicato per 4).