La velocità di propagazione delle onde elettromagnetiche
La determinazione della velocità di propagazione delle onde elettromagnetiche può essere fatta con un ragionamento abbastanza elementare, se si ammettono alcune loro caratteristiche, peraltro facilmente comprensibili anche a livello di studi liceali. L'idea è presa dal testo di Feynmann, The Feynmann lectures on Physics, con qualche semplificazione.
Consideriamo uno strato piano indefinito di carica, per esempio positiva, sovrapposto ad uno strato identico ma con carica di segno opposto (questo ci eviterà la complicazione della presenza di campi elettrostatici, sempre molto intensi e tali da nascondere gli effetti che interessano). Immaginiamo che all'istante t=0 lo strato di carica sia posto in moto con velocità v, verso la direzione positiva dell'asse y. (Per non essere costretti a pensare ad una accelerazione infinita, basterà pensare che la velocità passi da zero a v molto rapidamente). Il movimento dello strato di carica è equiparabile ad una successione di correnti continue rettilinee e parallele: la loro presenza produce un campo magnetico uniforme parallelo al piano di carica e orientato come l'asse z negativo. Ci si può rendere conto di ciò anche con un ragionamento elementare. Il variare di un campo magnetico, da un valore inizialmente nullo, quando lo strato di carica era fermo, ad un valore diverso da zero, quando lo strato di carica ha raggiunto la prevista velocità finale, provoca, secondo le equazioni di Maxwell, il sorgere di un campo elettrico, perpendicolare al campo magnetico e anch'esso uniforme, per questioni di simmetria.
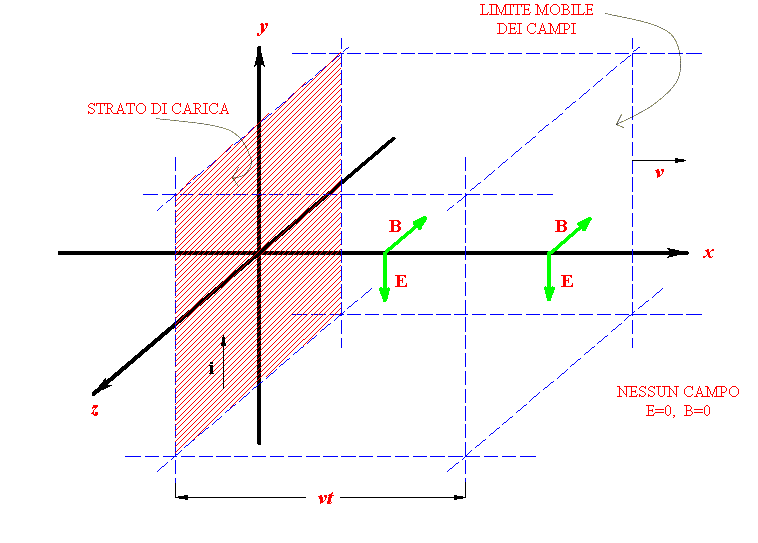
In sostanza il ragionamento porta a concludere che il passaggio dello strato di carica dalla quiete al moto provoca l'insorgere di un campo magnetico che, nella sua fase di variabilità iniziale, porta alla nascita di un campo elettrico. Poiché non è pensabile che, istantaneamente, tutto lo spazio sia occupato da un campo elettrico e da un campo magnetico, ci sarà una regione limite, per simmetria ancora piana e parallela al piano di carica, che delimiterà la zona dove i campi hanno un valore non nullo da quella dove i campi hanno ancora valore nullo. Anche se questa "deduzione" non è assolutamente banale, riteniamo sia accettabile dal punto di vista "elementare" che qui stiamo adottando. Questa "superficie di separazione" viaggerà con una velocità v che ci proponiamo di determinare.
Per determinare questa velocità applichiamo la terza e la quarta equazione di Maxwell a due opportuni circuiti, Γ1 e Γ2, di forma rettangolare, il primo nel piano xy, il secondo nel piano xz, e disposti in parte nella zona già raggiunta dai campi e in parte in quella ancora "vuota" di campo.
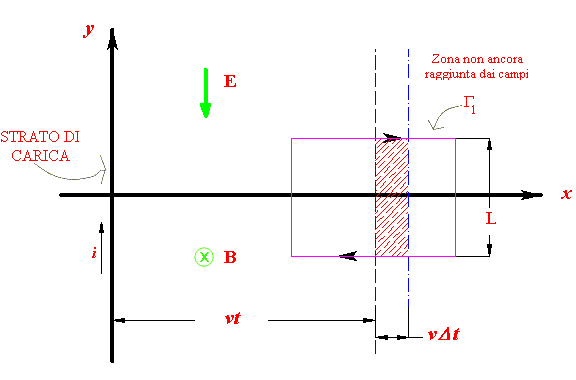
Cominciamo con il circuito Γ1, situato nel
piano xy, come nella figura qui sotto, e applichiamo
l'equazione 
. La circuitazione
di E dà subito -EL; per calcolare il secondo
membro basta osservare che 
; si trova quindi la relazione
E = vB
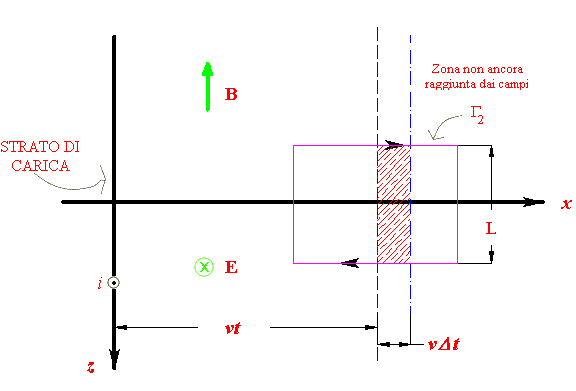
Consideriamo ora il circuito Γ2, situato nel
piano xz, come nella figura qui sotto, e applichiamo
l'equazione 
, dove abbiamo
tenuto conto che non ci sono correnti concatenate. Esattamente
con la stessa tecnica di sopra si trova che la circuitazione di
B è BL, il secondo membro è
ELvμ0ε0>. Si
conclude che
B=Evμ0ε0.
Combinando le due equazioni che abbiamo trovato (E = vB
e B=Evμ0ε0) troviamo
che 
, da cui la nota formula
per la velocità delle onde elettromagnetiche: 
.
In sostanza il quadrato della velocità delle onde
è il reciproco del prodotto
μ0ε0. É chiaro
che i valori delle due costanti μ0 ed
ε0 dipendono dalle unità di
misura scelte per la carica (o per la corrente a seconda della
scelta che si vuol fare come unità fondamentale); il loro
prodotto non dipenderà però dalle unità
scelte (il prodotto anziché il quoziente perché
nella definizione ε0 compare al
denominatore, mentre μ0 compare al
numeratore): se si raddoppia per esempio la carica unità,
ε0 dovrà diventare un quarto,
mentre se facciamo passare questa unità doppia di carica
in due fili la forza diventerà quadrupla e quindi
μ0 dovrà essere quadruplicata.
Quindi il valore di v può essere determinato
solo con esperimenti su cariche e correnti e, con misure
statiche, si ottiene che 
m/s. Quando Maxwell fece questi calcoli
notò subito che questa era la nota velocità della
luce e concluse con la storica frase: "sarebbe
difficile evitare la conclusione che la luce consiste di
oscillazioni trasversali del medesimo mezzo che è la
causa dei fenomeni elettrici e magnetici".