www.batmath.it

Spazio, Tempo, Spaziotempo

I nuovi postulati della relatività ristretta introducono il concetto di velocità assoluta (quella della luce): questo concetto è assolutamente estraneo alla meccanica Newtoniana (che aveva invece il concetto di accelerazione assoluta, per sistemi di riferimento in moto relativo rettilineo ed uniforme). É chiaro che l'introduzione di questo concetto dovrà produrre una radicale revisione delle nostre idee di spazio e di tempo, revisione già contenuta nelle trasformazioni di Lorentz, ma che si può capire ancora più a fondo se si esamina il cosiddetto orologio a luce.

Un orologio a luce può essere pensato come un dispositivo costituito da una sorgente A che manda un segnale luminoso verso l'alto, dove, a distanza λ, c'é uno specchio che riflette la luce verso il basso nel punto B, facendola ritornare in A. Nello stesso posto della sorgente c'é anche un rivelatore che vede il segnale riflesso, lo registra, e invia un nuovo segnale verso B. Ogni volta che il segnale ritorna in A viene emesso un ticchettio che rappresenta l'unità di tempo segnata dal nostro orologio. Un orologio simile è forse difficilmente realizzabile, ma ciò poco conta per i nostri scopi.. L'intervallo di tempo "base" del nostro orologio a luce sarà, dunque, il tempo impiegato dalla luce per andare da A a B e ritornare in A: lo indicheremo con  Δτ e lo chiameremo tempo proprio dell'orologio. Il tempo Δτ dipende esclusivamente dalla distanza sorgente-specchio e vale .

Immaginiamo ora che il nostro orologio sia in moto rispetto a noi, con una certa velocità v, "verso destra", e vediamo come ci appariranno le cose. Intanto dobbiamo osservare che, sulla base delle trasformazioni di Lorentz, la distanza λ tra sorgente e specchio non sarà modificata (in quanto le direzioni, y e z, perpendicolari alla velocità non sono influenzate dalle trasformazioni stesse). A questa stessa conclusione si sarebbe potuti anche arrivare direttamente sulla base dei postulati della relatività. 

Se indichiamo con Δx la distanza percorsa dall'orologio mentre il segnale luminoso va da A a B e ritorno, con Δt il tempo segnato dall'orologio del nostro laboratorio, e se teniamo conto che la luce viaggia sempre a velocità c, come prima, applicando il teorema di Pitagora al triangolo A₁B₂A₂, otterremo: 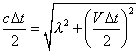. Da qui si può ricavare Δt e, ricordando il valore trovato per Δτ, si ottiene la formula seguente: . Questa famosa formula è nota come formula per la dilatazione dei tempi negli orologi in moto. Questo nome, forse più di effetto che di sostanza, è legato al fatto che da questa formula si deduce che se noi leggiamo, sul quadrante del nostro orologio nel laboratorio, l'intervallo di tempo che intercorre tra la partenza e il ritorno del segnale luminoso dell'orologio a luce, questo tempo (Δt) sarà più grande di quello (Δτ) segnato sul quadrante dell'orologio a luce: è come se, dal nostro punto di vista l'orologio in moto avesse rallentato. Non c'è nulla di strano o di misterioso in questo, tutto è legato al fatto che l'evidenza sperimentale ci ha costretto ad ammettere che la velocità della luce è uguale sia che la misuriamo dal punto di vista dell'orologio a luce, sia che la misuriamo dal punto di vista del laboratorio, nel quale l'orologio che emette e riceve il raggio di luce è in movimento. É chiaro che questo fatto non è facile da digerire, ma non c'è nulla da fare, visto che tutti gli esperimenti lo confermano con precisione praticamente assoluta. 

Ci si potrebbe chiedere perché nessuno ci ha mai pensato prima di Einstein, o comunque prima della fine del secolo scorso: il motivo è certamente da ricondurre al fatto che, nella pratica della nostra vita quotidiana , anche di sperimentatori nei laboratori scientifici, il fattore di correzione che rende il valore di Δτ diverso da quello di Δt è , cioè un valore estremamente piccolo, per velocità ordinarie. Come è noto, un tale  fattore di conversione è invece implicito nel concetto di magnetismo, anche se, all'origine, i fisici non si potevano rendere conto di questo fatto.

Supponiamo ora che il nostro orologio a luce si muova con una velocità v parallela al tratto AB. Con le stesse notazioni di prima, sul quadrante dell'orologio a luce troveremo lo stesso identico risultato: . Consideriamo ora la situazione che vede un osservatore nel laboratorio, rispetto al quale l'orologio è in moto verso destra con velocità v.

Nella figura qui sopra abbiamo rappresentato, dopo l'immagine dell'orologio a luce nel suo riferimento, tre successive posizioni dell'orologio a luce viste dal sistema del laboratorio (emissione del segnale, riflessione sullo specchio, ritorno alla sorgente) un po' sfalsate, per rendere più leggibile il disegno. Il lampo emesso dalla sorgente si riflette sullo specchio dopo aver percorso il tratto A₁B₂ e ritorna alla sorgente dopo aver percorso il tratto B₂A₃. Indichiamo con l la lunghezza dell'orologio misurata dall'osservatore solidale al laboratorio (che non sappiamo se sarà uguale a λ oppure no), con Δt₁ il tempo di "andata", con Δt₂ quello di "ritorno". Per trovare questi due tempi basterà che teniamo conto che, mentre il segnale viaggia, A e B si spostano, per effetto della velocità v. Si ha, facilmente, .  Da qui si possono ricavare i valori dei due intervalli di tempo che, sommati, danno il valore di Δt: .  Basterà ora ricordare il già trovato legame tra Δτ e Δt per ricavare la seguente formula: .

Questa formula è detta formula per la contrazione delle lunghezze di Lorentz-Fitzgerald, perché essa implica che la lunghezza l è più piccola della lunghezza λ. La contrazione delle lunghezze è perfettamente simmetrica alla dilatazione dei tempi e la cosa si può ben vedere nell'esperimento sui muoni usati come orologi.

    É da segnalare che queste formule hanno avuto una notevole importanza storica e sono, ancora oggi, normalmente presentate come due dei risultati chiave della teoria della relatività. In realtà, senza negare la loro importanza e il fatto che i concetti che esse esprimono sono, forse, due dei concetti più difficili da digerire e per questo più affascinanti soprattutto per i non addetti ai lavori, si potrebbe tranquillamente parlare di relatività senza mai parlare di dilatazione dei tempi e di contrazione delle lunghezze.

Molto più importante è il discorso che segue. Riprendiamo in considerazione una formula che ci è servita per ricavare la legge di dilatazione dei tempi: 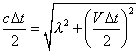.  Se scriviamo Δx al posto di VΔt (si tratta dello spostamento subito dall'orologio a luce nel laboratorio) e al posto di  λ, e ricaviamo Δτ, otteniamo: . Se considerassimo il moto dello stesso orologio con una diversa velocità, v', troveremmo diversi valori per Δx e Δt (rispettivamente Δx₁ e Δt₁), ma si avrebbe sempre , ovvero . Quadrando, riordinando e riducendo allo stesso denominatore si può ottenere la seguente conclusione fondamentale: . Questa formula esprime il fatto che mentre la lunghezza e il tempo, per proprio conto, dipendono dal riferimento, la combinazione è indipendente dal riferimento, cioè è un invariante. In relatività non si può parlare separatamente di spazio e di tempo, occorre parlare di spaziotempo.

Questo fatto è strano solo ad un'analisi superficiale, in realtà in geometria un fatto analogo è ben noto: se si considerano, in un piano, due diversi riferimenti cartesiani ortogonali e due punti A e B di coordinate (x_A,y_A), (x_B,y_B) e (X_A,Y_A) , (X_B,Y_B) nei due riferimenti, la loro distanza non dipende dal sistema di coordinate, ma il calcolo della distanza usando le coordinate cartesiane è diverso nei due riferimenti: . Questa formula esprime il fatto che la distanza è un invariante, mentre la differenza di ascisse e di ordinate non lo è. Tra questo invariante e quello della relatività ci sono due differenze: la presenza di c² (ma questa è una questione secondaria dipendente solo dalle unità di misura), e la presenza del segno meno davanti a c²Δt². Nonostante questo fatto la similitudine tra le due formule è così forte che essa ha dato origine a una trattazione "geometrica" della teoria della relatività (iniziata da Minkowski in un articolo del 1908).

L'idea che la relatività possa essere "ridotta" ad una sorta di teoria geometrica dello spazio tempo è di grande importanza e può, almeno entro certi limiti, essere considerata l'idea che sta alla base della teoria della relatività generale e di tutte le teorie di campo unificato che si sono succedute dopo la nascita della relatività generale.

copyright 2000 et seq. maddalena falanga & luciano battaia

pagina pubblicata il 01/12/2000 - ultimo aggiornamento il 01/09/2003