Relatività galileiana e trasformazioni galileiane
Il principio di relatività galileiana afferma l'assoluta equivalenza fisica di tutti i sistemi di riferimento inerziali: nessun esperimento eseguito all'interno di un dato sistema di riferimento può evidenziare il moto rettilineo ed uniforme dello stesso sistema, o, in altre parole, le leggi fisiche scoperte da sperimentatori che lavorino in laboratori in moto relativo rettilineo ed uniforme devono avere la stessa forma. Si tratta ora di ricavare le formule che legano le coordinate spazio temporali di uno stesso evento visto da due diversi riferimenti e di provare che le leggi della fisica sono invarianti, nella forma, al passaggio da un riferimento all'altro: si tratta cioè di tradurre in formule il contenuto di questo principio.
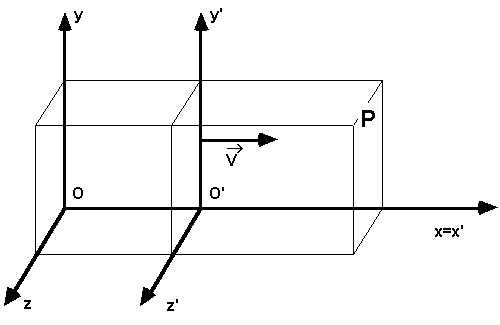
Si considerino due riferimenti, S ed S', di cui S'
mobile, rispetto ad S, di moto rettilineo ed uniforme, con
velocità 
. Si
supponga che gli osservatori solidali ad S e S' siano dotati
di due orologi per la misura dei tempi, preventivamente
sincronizzati in modo che, per esempio, quando O coincide con
O' entrambi gli orologi segnino zero. Non è
restrittivo prendere, come noi faremo, gli assi x dei due
riferimenti sovrapposti, in modo che sia parallela allo stesso asse x. Si
consideri un certo evento fisico che avviene in un punto P con
coordinate (x,y,z) e (x', y',z') rispetto a S e
S' rispettivamente, e negli istanti t e t' misurati dai
due osservatori. Tenendo conto che OO' = Vt e che sembra
ovvio supporre t'=t, dalla figura qui sopra segue subito che
valgono le cosiddette
Trasformazioni Galileiane: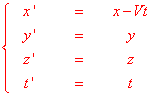 
Osserviamo in particolare che la quarta di queste formule è sempre stata ritenuta evidente, e lo è ancora nella vita pratica. La negazione dell'ipotesi (perché si tratta di un'ipotesi e non di una proprietà dimostrata sperimentalmente) che gli orologi dei due osservatori debbano segnare lo stesso tempo costituisce, come vedremo, uno degli aspetti innovativi della relatività Einsteniana.
Per derivazione si possono ottenere
le formule per la composizione delle velocità: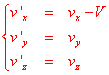 
.
Una ulteriore derivazione porta alla conclusione, fondamentale,
che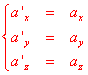 
.
Se teniamo conto del fatto che la massa dei corpi è un
invariante, utilizzando la equazione fondamentale della dinamica
(definizione di forza), 
, concluderemo che che la forma delle
equazioni non dipende dal riferimento. Una modifica delle
trasformazioni di Galileo deve portare necessariamente ad una
modifica della equazione fondamentale della dinamica, se
vogliamo salvare il principio di relatività. Questa
modifica costituisce uno dei tanti pilastri della teoria della
relatività che, occorre sottolinearlo fin dal principio,
non ha negato la validità del Principio di
relatività galileiana, ma solo delle formule di passaggio
da un riferimento ad un altro: il Principio è anzi stato
esteso a tutti i fenomeni e non solo a quelli meccanici.