Condensatori in moto
Consideriamo un condensatore piano mobile, in un dato
riferimento, con velocità v. Siano
l0 e w0 le sue
dimensioni misurate da un osservatore solidale al condensatore
(dimensioni a riposo). Poniamo, per questioni di
semplicità, u=v/c (ciò equivale a
misurare le velocità in "unità c");
avremo dunque v=uc. Le dimensioni misurate da un
osservatore solidale al riferimento saranno 
e w=w0. Supponiamo che le due
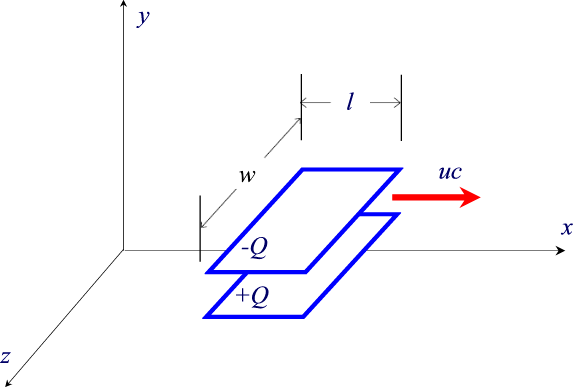
piastre siano caricate come nella figura qui sotto. Tra le
due piastre è presente un campo elettrico, uniforme,
diretto nel verso positivo dell'asse y e dato dalle formule:
.
Le due piastre in movimento costituiscono delle correnti e dunque generano un campo magnetico. Se supponiamo di dividere ognuna delle due piastre in tante striscioline parallelamente alla direzione del movimento, come nella figura qui sotto dove abbiamo rappresentato la situazione vista dall'alto, potremo pensare ad ognuna delle due piastre come ad un insieme di fili percorsi da corrente, messi vicinissimi uno all'altro.
Se N è il numero di suddivisioni, cioè di fili percorsi da corrente, la piastra negativa sarà percorsa da correnti nel verso negativo dell'asse x, quella positiva da correnti nel verso positivo.
Il condensatore sarà assimilabile ad un solenoide se
immaginiamo che ciascun filo sulla piastra negativa si chiuda a
circuito con il corrispondente della piastra positiva.
Come in un normale solenoide all'interno sarà presente un campo magnetico, uniforme, diretto nel verso positivo dell'asse z, e dato dalle formule (n rappresenta, al solito, il numero di spire per unità di lunghezza):
.
Per valutare la corrente i possiamo utilizzare il seguente
ragionamento: la carica Q contenuta su ognuna delle
piastre si sposta, verso la direzione positiva dell'asse x,
del tratto l nel tempo 
. La carica, q, contenuta su ognuna delle
suddivisioni è 
, dunque la corrente i è data da
. Per il campo B
si ottiene, tenendo anche conto che
w=w0: 
.
