Problemi riepilogativi di analisi delle funzioni reali di variabile reale - 3
Problema 51
-
In un piano riferito ad un sistema di coordinate cartesiane ortogonali xOy si consideri il punto A(-2,0). Si conduca per A una retta, r, avente un coefficiente angolare positivo. Delle due semirette individuate da A su r si consideri quella che giace nel semipiano delle ordinate positive e si indichi con α l'angolo, non maggiore di π/2, che essa forma con la direzione positiva dell'asse x. Si conduca poi una retta, s, per l'origine in modo che la semiretta individuata da O su s, che giace nel semipiano delle ordinate positive, formi un angolo 2α con la direzione positiva dell'asse x. Al variare di α in [0,π/2] si trovi il luogo Σ descritto dal punto P di intersezione delle due rette.
-
Detto B il punto di intersezione del luogo S con l'asse y e C quello, di ascissa positiva, con l'asse x, trovare l'equazione della cubica razionale intera avente massimo relativo in B e minimo relativo in C.
-
Detto D il punto di flesso della cubica si esegua una traslazione di assi che porti l'origine del sistema di coordinate in D e si deduca una proprietà di simmetria per la cubica.
-
Si trovi poi l'equazione della quartica razionale intera passante per A(-2,0) e avente massimo relativo in B e minimo relativo in C.
-
Dette f e g le funzioni che hanno grafico la cubica e la quartica, si risolva la disequazione f(x)>g(x), utilizzando i grafici ottenuti.
Problema 52
Sia n un intero maggiore di 1. Si considerino, al variare di n, le funzioni
![]() . Si dimostri che
tutte le funzioni ammettono come estremante un punto di scissa positiva. Si determini tale punto e
si dica se si tratta di massimante o di minimante. Posto n=2 si studi la funzione ottenuta.
Si esegua una traslazione di assi che porti l'origine nel punto O' di intersezione degli
asintoti della funzione e si deduca una proprietà di simmetria per la funzione stessa. Detta
Y=g(X) la nuova funzione, si trovi l'equazione della circonferenza di centro O' e
tangente al grafico della funzione.
. Si dimostri che
tutte le funzioni ammettono come estremante un punto di scissa positiva. Si determini tale punto e
si dica se si tratta di massimante o di minimante. Posto n=2 si studi la funzione ottenuta.
Si esegua una traslazione di assi che porti l'origine nel punto O' di intersezione degli
asintoti della funzione e si deduca una proprietà di simmetria per la funzione stessa. Detta
Y=g(X) la nuova funzione, si trovi l'equazione della circonferenza di centro O' e
tangente al grafico della funzione.
Problema 53
In un piano, riferito ad un sistema di coordinate cartesiane ortogonali xOy si consideri la
funzione ![]() ,
essendo m un numero reale. Dimostrare che tutte le curve grafico passano per uno stesso
punto di cui si chiedono le coordinate. Dire per quali valori di m le curva hanno un
massimo, per quali hanno un minimo e per quali non hanno né massimo né minimo. nel
caso in cui la curva ha un massimo o un minimo si determini il luogo geometrico descritto da questo
massimo o minimo al variare di m e lo si rappresenti.
,
essendo m un numero reale. Dimostrare che tutte le curve grafico passano per uno stesso
punto di cui si chiedono le coordinate. Dire per quali valori di m le curva hanno un
massimo, per quali hanno un minimo e per quali non hanno né massimo né minimo. nel
caso in cui la curva ha un massimo o un minimo si determini il luogo geometrico descritto da questo
massimo o minimo al variare di m e lo si rappresenti.
Problema 54
Si studi la funzione ![]() , determinando in particolare il punto di flesso. Si esegua una traslazione di assi
che porti l'origine nel punto di flesso e si deduca una proprietà di simmetria per la
f.
, determinando in particolare il punto di flesso. Si esegua una traslazione di assi
che porti l'origine nel punto di flesso e si deduca una proprietà di simmetria per la
f.
Problema 55
-
Si studi la cubica y = x3 - 5x2 +8x - 4, determinandone in particolare gli zeri, il segno, i massimi e minimi relativi, la concavità e convessità. Si calcoli l'area della regione finita di piano compresa tra la cubica e l'asse delle ascisse.
-
Utilizzando la cubica sopra considerata si determini l'equazione di una quartica razionale intera che abbia un minimo relativo per x = 1 e un flesso a tangente orizzontale per x = 2. Se ne tracci il grafico.
-
Tenendo conto del grafico ottenuto al punto b) si dica se una quartica razionale intera ha, in generale, un asse di simmetria.
-
Si consideri ora una generica quartica razionale intera y = ax4 + bx3 + cx2 + dx + e. Tenendo conto dei limiti agli estremi del dominio si dica se essa può avere un centro di simmetria. Si determini poi la condizione richiesta perché essa possa avere, invece, un asse di simmetria.
Problema 56
In un sistema di coordinate cartesiane ortogonali xOy sono date l'ellisse di equazione 16x2 + 25y2 = 1600 e la parabola di equazione 8x2 -45y = 0. Detto P il punto di intersezione delle due coniche, appartenente al primo quadrante, si calcoli l'area della regione finita di piano limitata dall'asse y, dall'arco OP di parabola e dall'arco BP di ellisse, essendo B il punto, di ordinata positiva, in cui l'ellisse incontra l'asse delle ordinate. Si trovi il volume del solido ottenuto dalla rotazione completa della predetta regione attorno all'asse delle x e di quello ottenuto da una rotazione completa attorno all'asse delle y. Si determini poi l'equazione della retta passante per P che divide la predetta regione in due parti equivalenti.
Problema 57
Si consideri un trapezio isoscele ABCD, di base maggiore AB, circoscritto ad una
circonferenza di centro O. Si indichi con E il punto di tangenza della base minore CD con la
circonferenza e si ponga EÔC=x. Sapendo che il trapezio è equivalente al
quadrato di lato ![]() , si determini, in funzione di
a ed x, il raggio della circonferenza.
Detti V e W rispettivamente il volume del tronco di cono e quello della sfera ottenuti facendo
compiere una rotazione di 180° attorno ad un diametro perpendicolare alle basi del trapezio,
rispettivamente al trapezio e alla circonferenza, si consideri la funzione y=W/V. Posto
tgx = X si studi la funzione ottenuta, nei limiti del problema, limitando
l'indagine alla derivata prima.
, si determini, in funzione di
a ed x, il raggio della circonferenza.
Detti V e W rispettivamente il volume del tronco di cono e quello della sfera ottenuti facendo
compiere una rotazione di 180° attorno ad un diametro perpendicolare alle basi del trapezio,
rispettivamente al trapezio e alla circonferenza, si consideri la funzione y=W/V. Posto
tgx = X si studi la funzione ottenuta, nei limiti del problema, limitando
l'indagine alla derivata prima.
Problema 58
-
Si consideri la funzione
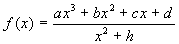 , essendo
a, b, c, d, h costanti reali. Si determini il valore delle predette
costanti affinché il grafico della funzione abbia per asintoto obliquo una retta di
coefficiente angolare 1 e per asintoto verticale la retta x=0, abbia, nel punto di ascissa
-2, per tangente la retta di equazione y=3x-6, abbia un minimo nel punto di ascissa
, essendo
a, b, c, d, h costanti reali. Si determini il valore delle predette
costanti affinché il grafico della funzione abbia per asintoto obliquo una retta di
coefficiente angolare 1 e per asintoto verticale la retta x=0, abbia, nel punto di ascissa
-2, per tangente la retta di equazione y=3x-6, abbia un minimo nel punto di ascissa
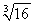 . Disegnare il
grafico della funzione così ottenuta determinando anche eventuali simmetrie.
. Disegnare il
grafico della funzione così ottenuta determinando anche eventuali simmetrie. -
Si determini l'equazione della tangente condotta al grafico per il suo punto P di ascissa -2; essa interseca la curva nell'ulteriore punto A. Si determini l'equazione di un'altra retta uscente da P e tangente alla curva nel primo quadrante in un punto T da determinarsi. Si trovi l'area della regione finita di piano compresa tra le due tangenti sopra trovate e l'arco AT di curva.
-
Considerata, della regione di cui al punto precedente, solo quella parte che giace nel semipiano delle x positive, si determini il volume del solido ottenuto facendo una rotazione completa attorno all'asse delle x.
Problema 59
Dato un numero reale a maggiore di zero, si consideri, in un piano π, un segmento
AB=9a. Si traccino poi la circonferenza di centro A e raggio a e la circonferenza di
centro B e raggio 2ka, essendo k un numero reale assegnato in modo che le due
circonferenze risultino non secanti. Detti rispettivamente C e D i punti di intersezione della
prima e seconda circonferenza con il segmento AB, sia P il punto medio di CD. Si conducano da P le
quattro semirette tangenti alle due circonferenze; esse individuano sulla prima circonferenza
l'arco MCN e sulla seconda l'arco ODR. In una rotazione di 180° attorno al
segmento AB questi archi generano due calotte sferiche di cui si chiedono le superfici riferentesi,
rispettivamente, al primo e secondo arco. Si consideri poi la funzione, nella variabile
k,
![]() . Si determini
il suo massimo e il suo minimo, nei limiti del problema.
. Si determini
il suo massimo e il suo minimo, nei limiti del problema.
Problema 60
Si consideri la funzione ![]() . Si determini il valore delle costanti reali
a, b, c, d, h in modo che il
grafico della funzione abbia per asintoto la retta x=1, per curva asintotica la parabola
y = x2 + x + 1 e che x=3/2 sia un punto estremante. Si
rappresenti la curva così ottenuta, studiando anche la derivata seconda. Si trovi l'area
della regione finita di piano compresa tra l'asse delle ascisse, il grafico della funzione, le
rette x=2 e x=5. Si trovi poi il volume del solido ottenuto in una rotazione completa
della predetta regione attorno all'asse delle ascisse. Utilizzando fin dove possibile i
risultati precedenti si rappresenti il grafico della funzione
. Si determini il valore delle costanti reali
a, b, c, d, h in modo che il
grafico della funzione abbia per asintoto la retta x=1, per curva asintotica la parabola
y = x2 + x + 1 e che x=3/2 sia un punto estremante. Si
rappresenti la curva così ottenuta, studiando anche la derivata seconda. Si trovi l'area
della regione finita di piano compresa tra l'asse delle ascisse, il grafico della funzione, le
rette x=2 e x=5. Si trovi poi il volume del solido ottenuto in una rotazione completa
della predetta regione attorno all'asse delle ascisse. Utilizzando fin dove possibile i
risultati precedenti si rappresenti il grafico della funzione
![]() .
.
Problema 61
Si consideri la funzione y = acos2x + bcosx, essendo a un numero reale positivo e b un numero reale qualunque. Si determinino i valori di a e b affinché il grafico della funzione passi per il punto (0,-1) e che il massimo assoluto della funzione valga 3 (si presti attenzione al fatto che è assegnato il valore del massimo e non il punto estremante). Si rappresenti poi il grafico della funzione ottenuta. Detta xM l'ascissa di uno dei punti di massimo assoluto, si verifichi, mediante una traslazione di assi, che la funzione è simmetrica rispetto alla retta x=xM.
Problema 62
Si studi la funzione ![]() , tracciandone un grafico indicativo. Si trovi poi una primitiva della funzione.
Detto t un numero reale maggiore di 1, si calcoli l'area della regione finita di piano
compresa tra la curva, l'asse delle x e le rette x=t e
x=t2.
, tracciandone un grafico indicativo. Si trovi poi una primitiva della funzione.
Detto t un numero reale maggiore di 1, si calcoli l'area della regione finita di piano
compresa tra la curva, l'asse delle x e le rette x=t e
x=t2.
Problema 63
-
In un piano π si considerino due circonferenze tangenti internamente in un punto S, una di centro O e raggio 1 e l'altra di centro O' e raggio a>1. Si consideri, nella circonferenza di centro O, una corda SM e si indichi con x l'angolo MŜO. Si tracci poi la bisettrice di MŜO: essa interseca la circonferenza di centro O n A e quella di centro O' in A'. Si conducano da S le due semirette perpendicolari rispettivamente ad SM ed SA: la prima incontri la circonferenza di centro O' in Q, la seconda la circonferenza di centro O in B e quella di centro O' in B'. Si consideri poi l'equazione B'A2 - A'B2 = SQ2; posto a2 = y si ricavi y in funzione di x e studi la funzione così ottenuta, limitando l'indagine alla derivata prima.
-
Supposto a costante, si studi la funzione f(x) = SM2 + SQ2, considerando anche la derivata seconda.
Problema 64
Sia data la funzione ![]() . Si determini il valore delle costanti reali
a e b in modo che la
funzione abbia come asintoto orizzontale la retta y=1 e come asintoto verticale la retta
x=2. Si studi poi la funzione ottenuta, limitando l'indagine alla derivata
prima.
. Si determini il valore delle costanti reali
a e b in modo che la
funzione abbia come asintoto orizzontale la retta y=1 e come asintoto verticale la retta
x=2. Si studi poi la funzione ottenuta, limitando l'indagine alla derivata
prima.
Problema 65
Si studi la funzione ![]() , determinando anche le equazioni delle rette tangenti nei punti di flesso.
, determinando anche le equazioni delle rette tangenti nei punti di flesso.
Problema 66
Si studi la funzione ![]() , fino a determinare, almeno per via grafica, il segno della derivata seconda.
, fino a determinare, almeno per via grafica, il segno della derivata seconda.
Problema 67
Si consideri, al variare del parametro reale m, la funzione
![]() .
.
-
Si trovi per quali valori di m la funzione ha sia un massimo che un minimo relativo. In questo caso si trovino i valori di m per i quali l'ascissa del massimo è minore di quella del minimo.
-
Si trovi per quali valori di m la funzione non ha massimi o minimi relativi.
-
Si provi che esiste un unico valore di m in corrispondenza del quale la funzione risulta avere un asse di simmetria. Si studi la funzione corrispondente a tale valore di m.
Problema 68
Si studino le funzioni y = x3 - 5x2 + 6x e y = -x3 + 3x2 - 2x, determinando anche i punti di intersezione dei grafici e il punto in cui sono tangenti. Fra le corde parallele all'asse delle y contenute nella parte finita di piano limitata dalle due curve si individui la corda CD di lunghezza massima. Si verifichi che le rette tangenti in Ce D alle due curve sono parallele.
Problema 69
Si consideri il fascio di circonferenze di equazione x2 + y2 - 2hx = 0, essendo h un numero reale non nullo. Si determini l'equazione delle parabole tangenti alla retta di equazione y=1, passanti per (0,0) e aventi l'ulteriore intersezione con l'asse x nel centro della generica circonferenza del fascio. Detti V e V' i vertici di due di tali parabole simmetriche rispetto all'asse y, si consideri l'area del triangolo mistilineo VOV' . Per quali parabole tale area vale 2/3?.
Problema 70
Tra tutte le funzioni che soddisfano la seguente equazione
![]() , si trovi quella che passa per
(0,0) e la si rappresenti graficamente.
, si trovi quella che passa per
(0,0) e la si rappresenti graficamente.
Problema 71
Si studi la funzione ![]() , limitando l'indagine alla derivata prima. Dette A e B le sue intersezioni con
la retta
, limitando l'indagine alla derivata prima. Dette A e B le sue intersezioni con
la retta ![]() , si
calcoli l'area della regione finita di piano individuata dall'arco AB, dalla parallela
all'asse x per l'estremo della funzione e dalle perpendicolari a questa passanti per
A e B.
, si
calcoli l'area della regione finita di piano individuata dall'arco AB, dalla parallela
all'asse x per l'estremo della funzione e dalle perpendicolari a questa passanti per
A e B.
Problema 72
Si studino, al variare di a, b, c le funzioni
![]() , ove c>0 e 0<a<b.
, ove c>0 e 0<a<b.
Problema 73
Si consideri l'equazione di secondo grado (k-1)x2 - 2(k+2)x + (k+1) = 0. Si dica per quali valori di k ha due radici positive. Si consideri poi il rettangolo R avente per dimensioni queste due radici. Si determini, in funzione di k, il volume della piramide avente per base il rettangolo R e per altezza il semiperimetro di R. Si studi la funzione così ottenuta.
Problema 74
É data la funzione f(x)= (cosx - a)2 +
b2sin2x, ove a e b sono costanti reali. Si
trovino i valori di a e b sapendo che f(0) = 0 e che
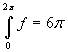 . Si studi la funzione
così ottenuta.
. Si studi la funzione
così ottenuta.
Problema 75
Data la funzione ![]() , si trovino i valori di
a e b in modo che la funzione abbia per
asintoto la retta x = -1 e passi per il punto A(2,0). Si determini poi l'area della
regione finita di piano compresa tra la curva, il suo asintoto obliquo e la retta
x=4.
, si trovino i valori di
a e b in modo che la funzione abbia per
asintoto la retta x = -1 e passi per il punto A(2,0). Si determini poi l'area della
regione finita di piano compresa tra la curva, il suo asintoto obliquo e la retta
x=4.