Problemi riepilogativi di analisi delle funzioni reali di variabile reale - 2
Problema 26
Si consideri la curva γ di equazione y = 4x3 - 3x -1, e se ne disegni il grafico indicando con A il punto in cui interseca il semiasse positivo delle ascisse. Determinare poi:
-
l'equazione della tangente a γ nel punto B di intersezione con l'asse delle ordinate e per quali valori dei coefficienti angolari m le rette per B sono secanti γ in altri due punti;
-
le equazioni delle tangenti a γ che sono perpendicolari alla retta 3x - 5y = 0;
-
l'area delle regioni finite di piano comprese tra la curva data e la parabola di equazione y = -2x2 + x +1;
-
Una retta appartenente al semipiano delle ordinate positive e parallela all'asse delle ascisse che, incontrando in M ed N la parabola data formi il triangolo AMN di area massima.
Problema 27
Si consideri la funzione ![]() .
.
-
Determinare i coefficienti non nulli a, b, c, d in modo che la retta y=1 sia un asintoto orizzontale, che la retta x=-3 sia un asintoto verticale e in modo che il grafico passi per i punti (2,0) e (5,0).
-
Tracciare il grafico della funzione, considerando anche la derivata seconda per la quale occorrerà determinare gli zeri per via grafica.
-
Trovare l'equazione della circonferenza tangente alla curva nel punto di ascissa 2 e con centro sulla retta x=-1.
-
Trovare l'area della regione finita di piano compresa tra la curva e l'asse delle x.
-
Detto t un reale tale che 0<t<2, calcolare
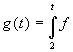 . Calcolare poi
. Calcolare poi 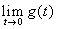 .
. -
Determinare l'equazione della retta, s, passante per i punti di massimo e minimo relativo della funzione. Determinare poi l'equazione delle parabole con l'asse parallelo all'asse delle ordinate, passanti per i suddetti punti di massimo e minimo relativo e tali che l'area della regione finita di piano compresa tra le parabole e la retta s sia uguale ad 1.
-
Considerata nuovamente la circonferenza trovata al punto c), indicare con A e B le sue intersezioni con l'asse x, essendo B il punto di ascissa positiva. Trovare l'equazione della parabola passante per A e B e tangente in B alla circonferenza. Si consideri la superficie limitata compresa tra la parabola e la retta passante per A e per il vertice della parabola. trovare il volume del solido ottenuto con una completa rotazione di questa superficie attorno all'asse x.
-
Considerata la curva di equazione y = ax3 + bx2 + cx -1/3, determinare i coefficienti a, b ,c in modo che essa sia una primitiva della parabola trovata al punto g). Tracciare poi il grafico della funzione così ottenuta.
Problema 28
Si consideri la funzione ![]() , con a, b, c costanti reali. Determinare le suddette costanti in modo che la
curva grafico della funzione in un sistema di coordinate cartesiane ortogonali abbia per asintoto
verticale la retta x=1/e, ed noltre abbia un minimo nel punto
, con a, b, c costanti reali. Determinare le suddette costanti in modo che la
curva grafico della funzione in un sistema di coordinate cartesiane ortogonali abbia per asintoto
verticale la retta x=1/e, ed noltre abbia un minimo nel punto 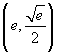 . Studiare la funzione
così determinata, prestando particolare cura allo studio della derivata seconda.
. Studiare la funzione
così determinata, prestando particolare cura allo studio della derivata seconda.
Problema 29
Un triangolo ABC di ortocentro H e di altezze AM, BN, CL, ha il lato AB di misura 1 e
l'angolo AĈB di π/3. Posto ABC=x si determini la funzione ![]() , dove si è posto
z
= cotanx. Si disegni il grafico della funzione.
, dove si è posto
z
= cotanx. Si disegni il grafico della funzione.
Problema 30
E' data una semicirconferenza di centro O e diametro MN=2r. Internamente ad essa, e con lo stesso centro O, si consideri una seconda semicirconferenza di raggio r/2. Su quest'ultima semicirconferenza si consideri un punto A e per esso si tracci la retta parallela al diametro MN. Essa incontri la prima semicirconferenza in C e D. Per C e D si traccino le tangenti alla semicirconferenza e sia P il loro punto di incontro. Congiunto P con O, si indichi con B il punto di intersezione tra OP e CD.
-
Posto BÔA=x si determinino i limiti per x. Si studi la funzione y = PB/AB in tutto il suo dominio, limitando l'indagine alla derivata prima.
-
Esprimere la funzione di cui in a) solo per mezzo di tanx. Porre quindi tanx = t e studiare la funzione così ottenuta.
-
Considerata ancora la funzione di cui in b), si tracci una retta per l'origine in modo che intersechi il grafico della funzione in due punto P e Q. determinare la posizione della retta in modo che la distanza tra P e Q sia minima. verificare che questa retta è la bisettrice dell'angolo formato dai due asintoti della curva.
-
Posto ancora BÔA=x si determini x in modo che l'area del triangolo CÔB sia massima.
-
Utilizzando i risultati ottenuti al punto b) studiare la funzione
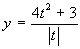 , determinando in particolare
eventuali punti in cui non è derivabile.
, determinando in particolare
eventuali punti in cui non è derivabile. -
Posto ora OB=x, studiare la funzione y=AB/CB, limitando l'indagine alla derivata prima.
Problema 31
Determinare le costanti a, b, c, d in modo che la funzione ![]() abbia come asintoto la retta
y=x, sia tangente alla retta
abbia come asintoto la retta
y=x, sia tangente alla retta ![]() , la quale, oltre al punto di contatto, ha in comune con la curva il punto
di ascissa -4/5. Tracciare il grafico della curva così ottenuta.
, la quale, oltre al punto di contatto, ha in comune con la curva il punto
di ascissa -4/5. Tracciare il grafico della curva così ottenuta.
Problema 32
Si considerino, al variare di k ≠ 0, le funzioni ![]() . Si dimostri che le funzioni hanno, al variare di
k, un massimo o minimo relativo in stesso punto di cui si chiedono le coordinate, precisando
per quali valori di k si ha un minimo e per quali si ha un massimo. Supposto poi
k>0, si determini k in modo che l'area della regione di piano compresa tra la
curva, l'asse delle x e le rette x=0 e x=1/2 sia 1.
. Si dimostri che le funzioni hanno, al variare di
k, un massimo o minimo relativo in stesso punto di cui si chiedono le coordinate, precisando
per quali valori di k si ha un minimo e per quali si ha un massimo. Supposto poi
k>0, si determini k in modo che l'area della regione di piano compresa tra la
curva, l'asse delle x e le rette x=0 e x=1/2 sia 1.
Problema 33
Si studi la funzione f(x) = xln|x| - 4x + 2, determinando anche l'equazione delle rette tangenti negli eventuali punti di flesso. Si dica se è possibili prolungare la funzione per continuità nel punto x=0.
Problema 34
Si consideri la funzione f(x) = x|x|. Si provi che il teorema di Rolle non è applicabile in nessun intervallo del dominio. Si mostri che ciò non implica la mancanza di un punto a derivata nulla.
Problema 35
Provare che la funzione ![]() verifica, nell'intervallo [1,2], il teorema di Lagrange e scrivere
l'equazione della tangente parallela alla corda passante per gli estremi dell'arco
assegnato.
verifica, nell'intervallo [1,2], il teorema di Lagrange e scrivere
l'equazione della tangente parallela alla corda passante per gli estremi dell'arco
assegnato.
Problema 36
Si consideri la funzione ![]() . Si determinino i valori della costanti a, b, c, h in modo che essa ammetta
per asintoto la retta
. Si determinino i valori della costanti a, b, c, h in modo che essa ammetta
per asintoto la retta ![]() e per curva asintotica la parabola y = -x2/2 + 2, e in modo
che abbia un minimo relativo nel punto di ascissa 1. Indicate con m ed
n le ascisse
dei punti di minimo, si trovi l'area della regione finita di piano limitata dalla curva,
dall'asse x e dalle rette x=n ed x=m.
e per curva asintotica la parabola y = -x2/2 + 2, e in modo
che abbia un minimo relativo nel punto di ascissa 1. Indicate con m ed
n le ascisse
dei punti di minimo, si trovi l'area della regione finita di piano limitata dalla curva,
dall'asse x e dalle rette x=n ed x=m.
Problema 37
Si riconoscano, al variare di k, le coniche: kx2 - (k+1)y2 - kx + 2y -1 = 0. Si provi che esistono due punti A e B comuni a tutte le curve. Si disegni la curva corrispondente al valore k = -1/2. Si operi una traslazione di assi che porti l'origine nel centro di simmetria della curva. Si disegni poi la curva corrispondente al valore k=-1 e si operi anche per essa la precedente traslazione di assi. Si calcoli infine l'area della regione finita di piano compresa tra le due curve.
Problema 38
Nella famiglia di funzioni per cui è y " = -cosx - 2sin2x, si individui quella che taglia l'asse delle ascisse nel punto x=π/2 e ha ivi per tangente la retta di equazione y = -2x + π. Si studi la funzione così ottenuta.
Problema 39
Si calcoli il ![]() ,
spiegando perché non è applicabile il teorema di l'Hôpital.
,
spiegando perché non è applicabile il teorema di l'Hôpital.
Problema 40
Si studi la funzione ![]() , limitando l'indagine alla derivata prima e determinando eventuali punti di non
derivabilità. Tra le parabole y = ax2 - 2ax + 3 si trovi
quella che interseca la curva nel punto B di ascissa 3. Si calcoli l'area, appartenente al
primo quadrante, racchiusa tra i grafici delle due funzioni (x è positivo e
quindi..).
, limitando l'indagine alla derivata prima e determinando eventuali punti di non
derivabilità. Tra le parabole y = ax2 - 2ax + 3 si trovi
quella che interseca la curva nel punto B di ascissa 3. Si calcoli l'area, appartenente al
primo quadrante, racchiusa tra i grafici delle due funzioni (x è positivo e
quindi..).
Problema 41
Si considerino le curve di equazione ![]() . Si dimostri che è possibile operare una traslazione di assi in
modo che esse si possano mettere nella forma Y = c/X, con un opportuno valore
di c. Si deduca che le curve sono simmetriche rispetto ad un punto A e si determini il luogo
descritto da A al variare di k. Si individui, tra le curve, quella che ha asintoto
orizzontale y=1. Si determini l'area della regione finita di piano compresa tra la curva
così trovata, il luogo dei punti A, e la retta x=1. Detti poi B e C i punti in cui le
curve date tagliano l'asse delle x e delle y rispettivamente, si studi la
variazione della distanza tra C e B, in funzione di k.
. Si dimostri che è possibile operare una traslazione di assi in
modo che esse si possano mettere nella forma Y = c/X, con un opportuno valore
di c. Si deduca che le curve sono simmetriche rispetto ad un punto A e si determini il luogo
descritto da A al variare di k. Si individui, tra le curve, quella che ha asintoto
orizzontale y=1. Si determini l'area della regione finita di piano compresa tra la curva
così trovata, il luogo dei punti A, e la retta x=1. Detti poi B e C i punti in cui le
curve date tagliano l'asse delle x e delle y rispettivamente, si studi la
variazione della distanza tra C e B, in funzione di k.
Problema 42
Si dimostri che ogni cubica razionale intera ha un centro di simmetria. Si verifichi poi che tale centro è l'unico punto di flesso della curva. Si spieghi perché una cubica ha sempre un unico punto di flesso.
Problema 43
Si consideri la funzione ![]() . Si scriva l'equazione della tangente al suo grafico in un punto di ascissa
c. Detto t un numero reale, si determini il numero delle tangenti condotte alla curva
grafico della funzione dal punto P(0,t). Si verifichi in particolare che esiste una sola
tangente condotta per l'origine. Utilizzando i risultati ottenuti si determini il numero delle
intersezioni tra il grafico della funzione e la retta y = mx - 4, essendo
m un numero
reale.
. Si scriva l'equazione della tangente al suo grafico in un punto di ascissa
c. Detto t un numero reale, si determini il numero delle tangenti condotte alla curva
grafico della funzione dal punto P(0,t). Si verifichi in particolare che esiste una sola
tangente condotta per l'origine. Utilizzando i risultati ottenuti si determini il numero delle
intersezioni tra il grafico della funzione e la retta y = mx - 4, essendo
m un numero
reale.
Problema 44
Si dica per quali x è derivabile la funzione ![]() .
.
Problema 45
Si consideri la funzione 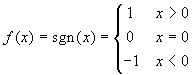 . Si dica se la funzione |f(x)| è derivabile per
x=0. Si dica se
è possibile scegliere una funzione y = g(x) in modo che la funzione composta
y = |sgn(g(x))| sia derivabile per x=0. si dica infine se
quest'ultimo risultato è in contrasto con il teorema sulla derivabilità delle
funzioni composte.
. Si dica se la funzione |f(x)| è derivabile per
x=0. Si dica se
è possibile scegliere una funzione y = g(x) in modo che la funzione composta
y = |sgn(g(x))| sia derivabile per x=0. si dica infine se
quest'ultimo risultato è in contrasto con il teorema sulla derivabilità delle
funzioni composte.
Problema 46
Si consideri la funzione 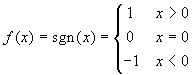 . Si dica se è derivabile per x=0. Si dimostri che la funzione
f(x)=x2sgn(x) è derivabile per
x=0. Questo
risultato è in contrasto con qualcuno dei teoremi sulla derivabilità?
. Si dica se è derivabile per x=0. Si dimostri che la funzione
f(x)=x2sgn(x) è derivabile per
x=0. Questo
risultato è in contrasto con qualcuno dei teoremi sulla derivabilità?
Problema 47
Si consideri la funzione ![]() . Si determini il valore delle costanti reali a, b, c, d in modo che il
grafico della funzione passi per il punto (0,0) e che abbia per asintoti le rette
x=2 e
y=3. Si esegua una traslazione di assi che porti l'origine nel punto di intersezione
degli asintoti. Che proprietà se ne deduce per la funzione data? Si esegua, successivamente,
una rotazione di assi che porti l'asse delle x a coincidere con una delle bisettrici
degli angoli individuati dagli asintoti. Che proprietà se ne deduce per la funzione
data?
. Si determini il valore delle costanti reali a, b, c, d in modo che il
grafico della funzione passi per il punto (0,0) e che abbia per asintoti le rette
x=2 e
y=3. Si esegua una traslazione di assi che porti l'origine nel punto di intersezione
degli asintoti. Che proprietà se ne deduce per la funzione data? Si esegua, successivamente,
una rotazione di assi che porti l'asse delle x a coincidere con una delle bisettrici
degli angoli individuati dagli asintoti. Che proprietà se ne deduce per la funzione
data?
Problema 48
Si studi la funzione ![]() , limitando l'indagine alla derivata prima e calcolando anche il limite della
derivata prima quando x tende ad 1.
, limitando l'indagine alla derivata prima e calcolando anche il limite della
derivata prima quando x tende ad 1.
Problema 49
Sia data una circonferenza di centro O e raggio r. Si consideri la corda
AB=(8/5)r. Si conduca dal punto B la semiretta tangente alla circonferenza e situata,
rispetto alla retta AB, nel semipiano contenente il centro. Su detta semiretta si consideri un
punto P e si ponga PÂB=x. Detto M l'ulteriore punto di intersezione di AP con la
circonferenza, si studi, nei limiti del problema, la funzione ![]() .
.
Problema 50
Sia f(x) una funzione definita per x>0. Si determini f sapendo che f '(x)=xex e che l'equazione f(x) - lnx - x2 = 0 ammette la radice x=1.