Problemi di massimo e minimo
Problema 1
Un ragazzo che si trova in un punto A, situato lungo un rettilineo di una strada di campagna, deve raggiungere la propria ragazza che si trova (ad aspettarlo ansiosamente) in un casolare situato in un punto B, distante 8 km dalla strada, in mezzo ad un prato. La distanza in linea d'aria tra A e B è di 17 km. Il ragazzo può correre a 5 km/h sulla strada e a 3 km/h sull'erba del prato. In quale punto dovrà abbandonare la strada se, come è naturale, vuole raggiungere la propria ragazza nel più breve tempo possibile?
Problema 2
Un furgone deve percorrere 600 km su una strada alla
velocità costante di x km/h. I limiti di
velocità impongono che la velocità minima sia di
60 km/h, e quella massima di 120km/h. Si supponga che le benzina
costi 1300 £it al litro (!!) e che si consumino 
litri all'ora. Se la paga dell'autista è
di 10000 £it all'ora, si chiede qual'è la
velocità che rende minimo il costo del viaggio
nell'ipotesi che l'autista rispetti i limiti di
velocità.
Problema 3
Con riferimento alla figura di seguito riportata, si consideri una casa sufficientemente alta e un muro alto 2 metri e distante 2 metri dalla casa. Una persona vuole costruire una scala, da disporre appoggiata al muro come in figura, in modo da poter toccare la casa con la punta delle dita, dopo essere salita in cima. Si supponga che, in totale, la persona possa sporgersi di 1 metro dalla scala. Si chiede qual'è la scala di lunghezza minima che deve essere costruita.
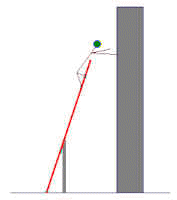
Problema 4
Siano A, B, C tre punti allineati, con B tra A e C e con AB=2 e BC =1. Si consideri una circonferenza passante per A e B e sia O il suo centro. Detta H la proiezione di O su AB, si ponga OH=x. Condotte da C le tangenti alla circonferenza, si determini quella circonferenza per cui l'angolo 2γ formato dalle suddette tangenti è minimo.
Problema 5
Si consideri una piramide retta, a base quadrata ABCD e
di vertice V, i cui spigoli misurano 
. Indicato con x l'angolo 
, del piano contenente AV e VB, si
determini, in funzione di x, il Volume V(x)
della piramide. Indipendentemente dal problema geometrico
proposto si studi la funzione y=V(x) in tutto il suo
dominio naturale e se ne deduca il massimo volume per la
piramide assegnata.
Problema 6
E' dato un triangolo isoscele ABC, rettangolo in A e di cateto a. Per il vertice C si conduca una retta CX esterna al triangolo e formante un angolo x con il cateto AC. Calcolare x in modo che risulti massimo il volume del solido generato dal triangolo ABC in una rotazione completa attorno a CX.
Problema 7
Si consideri la parabola y = x2 - 1. Sia V il suo vertice e A il punto di intersezione, ad ascissa positiva, con l'asse delle x. Si consideri una retta, normale ad AV, che intersechi la parabola in due punti P e P'. Si trovi il massimo e il minimo dell'area PAP'V, al variare della retta sopra considerata.
Problema 8
Si disegnino le due curve di equazione 
e
, trovando in particolare i loro punti
comuni. Si determini una retta di equazione x=p in modo
che intersechi la prima curva nel primo quadrante in un punto M
e che, detto N il punto di intersezione con la seconda curva, si
abbia:
- MN sia massimo.
- Il rettangolo che ha per lati opposti MN e la sua proiezione M'N' sull'asse y abbia area massima.
Problema 9
Si consideri la funzione 
. Sia P un punto
appartenente al grafico di questa funzione e si conduca per P la
tangente al grafico: essa forma un angolo α con l'asse
delle x (con le solite convenzioni). Trovare P in modo
che |tanα| sia massimo. Si spieghi perché si
trovano due punti P che soddisfano alla proprietà
richiesta.
Problema 10
Si consideri il settore circolare AOB di centro O, raggio r e ampiezza α (<90°). Sull'arco AB si prenda un punto P e da esso si conducano le parallele ai lati OA ed OB fino ad incontrarli nei punti E e D rispettivamente. Determinare la posizione del punto P in modo che l'area del parallelogramma OEPD sia massima.
Problema 11
E' data una semicirconferenza di diametro AB=2r. Si conduca da A una corda AM e si prenda su AB un punto N in modo che AM=AN. assunto come incognita l'angolo MÂN, determinare:
- Il triangolo AMN di area massima.
- Il triangolo AMN di perimetro massimo.
Problema 12
Fra tutti i triangoli rettangoli di data ipotenusa, a, determinare quello per cui risulti massima la somma dell'altezza relativa all'ipotenusa e della proiezione del cateto sull'ipotenusa.
Problema 13
E' dato il triangolo isoscele ABC la cui base AB misura
6a e in cui l'angolo BÂC ha il coseno uguale
a 3/5. Considerato sul lato BC un punto P e posto
BÂP=x, si determini P in modo che 
sia minimo, essendo M il punto medio di AB.
Problema 14
Sia ABC un triangolo inscritto nella circonferenza di centro O e raggio 1. Dato l'angolo BÂC=α, si ponga uguale ad x l'angolo ABC. Si determini, in funzione di α ed x, l'area del triangolo dato. Si dimostri che detta area assume valore massimo quando il triangolo è isoscele e si trovi il valore di questo massimo: esso dipende solo da α, lo si indichi con M(α). Utilizzando la funzione M(α), si provi che tra tutti i triangoli isosceli quello di area massima è l'equilatero.
Problema 15
Si consideri un quadrante AOB di circonferenza di centro O e raggio r. Sia M il punto medio di OA. Sia P un punto dell'arco AB. Posto AÔP=x si determini P in modo che il quadrilatero OMPB abbia area massima. Detto α il valore di AÔP che realizza il massimo si costruisca, con riga e compasso, il quadrilatero corrispondente.
Problema 16
Sia AB un segmento lungo a. Con centro in A si tracci una circonferenza di raggio minore di a. Dal punto B si traccino le tangenti alla circonferenza e siano M ed N i punti di contatto. Si determini l'angolo MBN=2x in modo che
- il volume del cono ottenuto da una rotazione di 180° del triangolo BMN attorno ad AB sia massimo;
- l'area della superficie la laterale del predetto cono sia massima.
Problema 17
Si dimostri che l'equazione 81x4 + 72x - 64 = 0 ha due soluzioni, una positiva e una negativa, e si determini quella positiva sapendo che è razionale. Si consideri poi l'iperbole di equazione xy = 8/9. Si trovi l'equazione della circonferenza avente centro nel punto (0,1) e tangente all'iperbole nel primo quadrante. (Si osservi che basta trovare il punto dell'iperbole che realizza la minima distanza da...).
Problema 18
Sia data la parabola y = (1/4)x2 ed un generico punto A(0,b), con b>0. Si trovi la minima distanza tra A ed un generico punto della parabola.