The key to this problem is to measure, after each second,  the fraction of the rope's length travelled by the worm in that second. It's easy to conclude that:

• in the first second the fraction of the length travelled is .
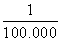• in the next second the fraction is .
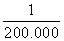• in the third second the fraction is .
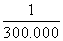• and so on...

So the worm can reach the end of the rope only if the sum of all these fractions is 1. The trouble is that the addenda become smaller and smaller. In order to estimate the sum we prefere to write it like this:

.

Now consider the sum between brackets. It is not easy to make this calculation, but in order to obtain some information we can group the terms in the following way: . The sum of the terms in each parenthesis exceeds : for example .  Observe that when the sum is written in this form:

• the first addendum is 1;
• there is one (2⁰) addendum whose value is 1/2;
• there are two (2¹) addenda in the first bracket, and the last addendum has denominator 2²;
• there are four (2²) addenda in the second bracket, and the last addendum has denominator 2³;
• and so on...

So when you have 199.999 addenda the sum is certainly beyond 100.000 and the last addendum has denominator 2^200.000. Certainly much before 2^200.000 seconds the worm reaches the end of the rope.

This is a very rough estimate, a better one (that is not so easy to obtain) is e^100.000.

If you continue adding terms to this sum, you can exceed every fixed value: if the number of terms becomes infinite you obtain what in mathematics is called a series. The case here considered is of particular importance in applications and is called the harmonic series. Mathematicians call series like the one in this puzzle divergent series (in order to distinguish them from the convergent series).