What functions are Riemann integrable?
To get further we now want to find a rule to decide if a function is Riemann integrable. The problem is not simple: from the very beginning it is evident that also discontinuous functions may be integrable (step functions are usually discontinuous!). We'll consider some of the main theorems, without proof.
The first theorem states a general condition to characterize Riemann integrable functions.
Theorem
A bounded function f(x) is Riemann integrable in an interval [a,b] if and only if, given a strictly positive number ε, it is possible to find two step functions s and t, such that:
for all x in [a,b],
s(x)≤f(x)≤t(x)
.
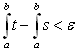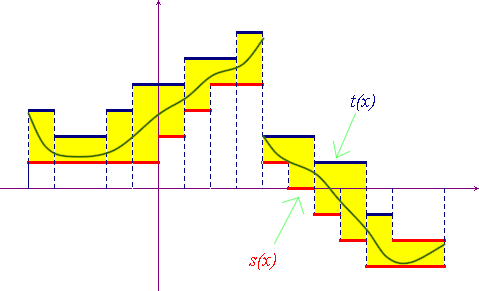
This theorem has a simple geometric interpretation: a function is Riemann integrable if and only if its graph can be enclosed in a finite number of rectangles, as shown in the picture below, whose total area is less than a fixed positive number ε.
The next two theorems are of the utmost importance, as almost all functions currently used in applications are monotòne or continuous.
Monotòne functions are integrable
Every monotòne function on an interval [a,b] is integrable in [a,b].
Obviously the condition of this theorem is not necessary: step
functions are always integrable, but they are usually not
monotòne.
Continuous functions are integrable
Every continuous function on an interval [a,b] is integrable in [a,b].
Also the condition of this theorem is not necessary: step functions are always integrable, but they are usually not continuous.
As repeatedly observed also discontinuous functions may be integrable. However a function such as Dirichlet's one is not integrable: it is too much discontinuous, so its graph cannot be enclosed in a finite number of rectangles of total area sufficiently small.
The following theorem is probably the most important one as far as integrability is concerned: it marks out the integrable functions on the basis of the amount of discontinuities allowed. Unfortunately it is not a simple theorem and a previous definition is needed.
Negligible sets
A subset A of real numbers is negligible, in the sense of Lebesgue, if, given a strictly positive number ε, it is possible to consider a (at the most) countably infinite set of intervals whose total length is less than ε, and whose union contains A.
Now we are ready to introduce the promised theorem.
The Vitali-Lebesgue Theorem
A bounded function 
is Riemann integrable if
and only if the set of its discontinuities is negligible
For usual applications the main consequence of this theorem is that functions that have a finite or a countably infinite set of discontinuities are Riemann integrable.
The integrability of continuous functions is an obvious consequence of this theorem, but also the integrability of monotòne functions, as one can prove that a monotòne function has at least a countably infinite set of discontinuities.