www.batmath.it di maddalena falanga e luciano battaia

www.batmath.it

Home page > Section in English > The Riemann Integral > Fundamental theorem of the integral calculus > Continuity of the integral function

The differentiability of the integral function

Given a point d where the function f is continuous, let's calculate the incremental ratio of the function . We use some properties of the Riemann integral and the mean value theorem.

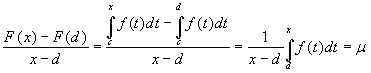
where μ is the mean value of the function f between x and d. This value is enclosed between the infimum and the supremum of the function in the interval [x,d] or [d,x]. The continuity of the function implies that μ tends to f(d) as x tends towards d. This proves the theorem.

Home page > Section in English > The Riemann Integral > Fundamental theorem of the integral calculus > Continuity of the integral function

first published on january 07 2003 - last updated on september 01 2003