Matrices and systems of linear equations
Row-echelon form
A matrix is in row-echelon form if:
- all zero rows (if any) are at the bottom of the matrix
- if two successive rows are non-zero, the second starts with more zeros than the first (moving from left to right).
The leading (leftmost non-zero) entry of a row (if any) is called a pivot.
A matrix is in reduced row-echelon form if it is in row-echelon form and
- the pivot entry in each non-zero row is 1
- all other elements of the column in which the leading entry 1 occurs are zeros.
Examples
-
The matrix
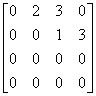is in row-echelon form.
-
The matrix
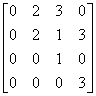is not in row-echelon
form.
-
The matrix
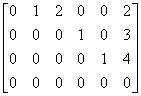is in reduced
row-echelon form.
-
The matrix
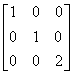and the matrix 
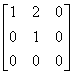are not in reduced row-echelon form.
Elementary row operations
The following three operations are called elementary row operations:
- Interchanging two rows: Ri↔Rj interchanges rows i and j.
- Multiplying a row by a non-zero scalar: Ri→cRi multiplies row i by the real number c.
- Adding a multiple of one row to another row: Ri→Ri+ cRj adds c times row j to row i.
Matrix A is row-equivalent to matrix B if B is obtained from A by a sequence of elementary row operations.
Example
Given the matrix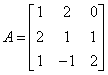 
; R2
→ R2 + 2R3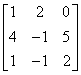 
; R2 → R3
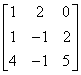; R1 →
2R1 
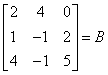. A
and B are row-equivalent.
It's not difficult to prove that if A and B are row-equivalent augmented matrices of two systems of linear equations, then the two systems have the same solutions set: solving one of the two systems is exactly the same thing.
The Gauss-Jordan algorithm
This is a process that starts with a given matrix A and produces a matrix B in (reduced) row-echelon form, which is row-equivalent to A. Reduced row-echelon form is better, but row-echelon form is enough for almost all purposes. If A is the augmented matrix of a system of linear equations, then B will be a much simpler matrix than A from which the consistency or inconsistency of the corresponding system is immediately apparent and in fact the complete solution of the system can be read off. As we want to apply this process to the solution of linear systems we assume that there are no zero rows in the original augmented matrix (a zero row means a meaningless equation).
This process is made up of the following steps:
- Step 1. Find the first non-zero column moving from left to right (usually there are no zero columns, otherwise the corresponding unknown is useless, but it is better to consider this more general case).
- Step 2. By interchanging rows, if necessary, ensure that the first entry in this column is non-zero: this leading entry is the first pivot, p1.
-
Step 3. Use the third elementary
row operation to obtain all zeros "under" this
pivot. You can proceed as follows: if the row number
i has a non zero entry, say a, under the
pivot, multiply the first row by
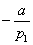and add it to row number i.
- Step 4. Repeat the process to the matrix you obtain by deleting row 1, until you obtain the row-echelon form.
- Step 5. If you are interested in the reduced row-echelon form, divide each row by the pivot and suitably use the third elementary row operation.
Systematic solution of linear systems
Suppose a system of m linear equations in n unknowns x1, x2, ..., xn has augmented matrix A|b. Via the Gauss-Jordan algorithm transform the matrix A|b in a matrix B|c with B in row-echelon (or reduced row-echelon) form. The number of pivots in the matrix B is called the rank, r, of the system, and we must have r≤min(m,n).
Once the augmented matrix is so reduced the consistency or inconsistency of the system can immediately be checked:
- The system is consistent if and only if in correspondence to all zero rows (if any) in the matrix B, the corresponding constants are zero.
Also the number of solutions can immediately be checked.
- If r=n there is a unique solution, that can be easily found if the system is in reduced row-echelon form.
- If r<n there are infinitely many solutions: there are columns without pivot and the corresponding unknowns can take on arbitrary values and may be considered as independent unknowns. The other unknowns (dependent unknowns) are expressed in terms of the independent ones. It's usual to say that there are ∞n-r solutions, to point out the fact that exactly n-r unknowns remain completely unspecified.
Homogeneous systems
If all constants are zero the system is called homogeneous. A homogenous system is always consistent as it has at least the trivial solution (0, 0, ... ,0). It also has other non trivial solutions if m<n.
Homogeneous systems play an important role in the theory of linear functions between vector spaces.